



Di una donna mi colpiscono soprattutto le mani. Ho ancora i segni nelle guance
OTTICA TEORICA

CONVOLUZIONE
Si consideri un oggetto con una distribuzione delle intensità di radiazione data da
seguito da un sistema ottico che crei una immagine . Le informazioni sull'oggetto
sono trasformate in informazioni sulla immagine tramite un processo che matematicamente
può essere rappresentato come



La funzione è detta funzione dilatazione del punto. In effetti ogni punto
sorgente dell'oggetto compare nel plano dell'immagine come una specie di macchia di luce.
La configurazione esatta della macchia (cioè la risposta all'impulso) è determinata
dal particolare sistema ottico.
(Nel caso di un sistema di lenti perfetto, ad esempio. S sarebbe una figura di Airy).
L'integrale si limita a sommare tutte queste macchie di luce dando quindi la
immagine risultante.
Così se si mette un pezzettino di carta davanti alla lente di una macchina fotografica,
l'immagine di una sorgente puntiforme, cioè la funzione dilatazione del punto, viene
certamente cambiata, e quindi ogni fotografia ne viene di conseguenza influenzata
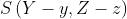
La espressione sopra introdotta rappresenta un integrale di convoluzione su due
dimensioni e il procedimento è detto di "convoluzione" delle due funzioni. Più concisa-
-mente, l'integrale può essere scritto come
Geometricamente la convoluzione può essere considerata come il volume racchiuso
dalla superficie prodotto che delimita la regione di sovrapposizione
delle due funzioni.
Nel campo unidimensionale, la convoluzione è la area della superficie
di sovrapposizione sottesa dal prodotto delle due funzioni

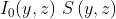

1 )
La funzione cilindro o tuba P(r) della sottostante figura, è una estensione bidimen-
-sionale della funzione impulso unitario. Determinare l'autoconvoluzione,
e tracciarne il diagramma in funzione della
variabile di posizione R.
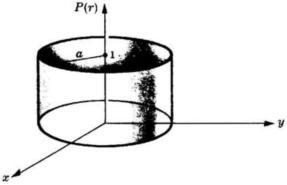


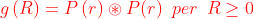
Dato che l'altezza di P( r ) è 1, la convoluzione
è semplicemente l'area di sovrapposizione della
sottostante figura geometrica, come funzione di
R. L'area di uno dei due segmenti (ACBA o ACDA)
è eguale all'area del settore OABCO meno l'area
del triangolo AOC, cioè

il doppio di questo è l'area di sovrapposizione A

Per esprimere A in funzione di R si usi la relazione
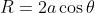
valevole per . Quindi per ,



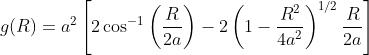
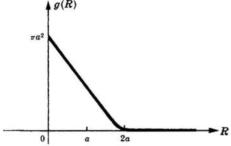
Quando , mentre per un valore di
(nessuna sovrappo sizione).
Il grafico della funzione è dato nella figura a lato.
il caso affrontato è particolarmente importante perchè
è strettamente collegato alla funzione di trasferimento ottico di una lente ideale.



2)
Il teorema della convoluzione afferma che se ,
cioè la trasformata di una convoluzione di due funzioni è il prodotto delle
trasformate delle singole funzioni. Dimostrare il teorema.


La convoluzìone g è una funzione di X e quindi la sua trasformata è
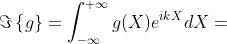
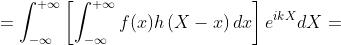

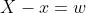
Posto , si ha e quindi
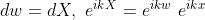


3)
La sottostante figura rappresenta una funzione coseno f(x) e la sua trasformata di
Fourier F(k). Costruire graficamente la autoconvoluzione di F(k).


In generale, per costruire , si
considera f composta da una serie di
funzioni delta, ognuna delle quali è quindi
allargata nella forma di h con la origine
nella posizione della funzione delta.
La somma dei contributi di tutte le funzioni
delta è quindi g.
Il procedimento risulta particolarmente facile
in questo caso, dato che la funzione su cui
lavorare è effettivamente composta di funzioni
delta.
Quindi si disegna allargata in due
funzioni delta come in figura (b ), ed analo-
-gamente viene allargata come in
figura ( c).
La somma di (b) e ( c) dà l’autoconvoluzione
raffigurata in (d).

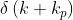


4)
Usare il procedimento illustrato nel precedente problema, per costruire la
autoconvoluzione di un impulso quadrato largo d.
Dalla proprietà di filtro della funzione delta del precedente problema, segue che una
funzione può essere rappresentata come somma lineare di impulsi. La parte sinistra
della sottostante figura, presenta l'impulso quadrato come risultato di un certo
numero di funzioni delta. Ognuna di queste, a sua volta, funziona come centro di un
impulso quadrato riprodotto nella parte destra della figura.
La somma di tutti questi è quindi la convoluzione.
In altre parole, ogni funzione delta costitutiva di f è allargata in un impulso quadrato
corrispondente a h. In questo caso ovviamente f e h sono identiche.
Portando il procedimento al limite di un numero infinito di funzioni delta, si vede che
la convoluzione g è un triangolo avente base 2d e alto d volte la altezza dell'impulso
quadrato.



Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





