



Chi disprezza il prossimo si preoccupa già troppo del prossimo
OTTICA TEORICA

DIFFRAZIONE DI FRESNEL - SPIGOLI RETTILINEI
DIFFRAZIONE DI FRESNEL - SPIGOLI RETTILINEI
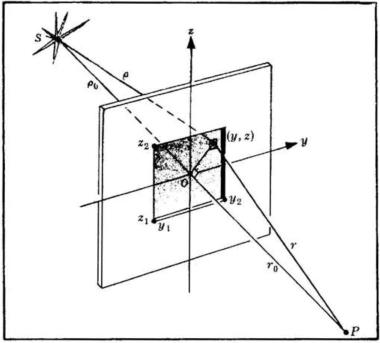
Prendiamo ora in esame la diffrazione di
Fresnel dovuta a sistemi limitati da spigoli
rettilinei, come fori rettangolari, fenditure,
fili, ecc. La figura a lato presenta un dispo-
-sitivo tipico del genere.
Per determinare il campo in P si determina
anche in questo caso l'integrale rispetto
alla intera apertura di tutti i contributi ele-
-mentari, partendo dalla ipotesi che ogni
elemento di superficie emetta una onda
secondaria.
Si assume eguale a uno il fattore di obli-
-quità, dato che si suppone che l'apertura
sia piccola rispetto a .Il termine
che figura nella fase è approssimato
come



che è una espressione del secondo ordine rispetto alle variabili che caratterizzano
l'apertura. Si assume come valore di da cui dipende la ampiezza delle onde
secondarie il valore . Si introducono le grandezze adimensionali

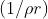

e si trova che il campo in P è

Il coefficiente che moltiplica l'integrale è pari alla metà della perturbazione che si ha
in P nel caso non vi siano ostruzioni; lo si indichi con . Il valore degli integrali può
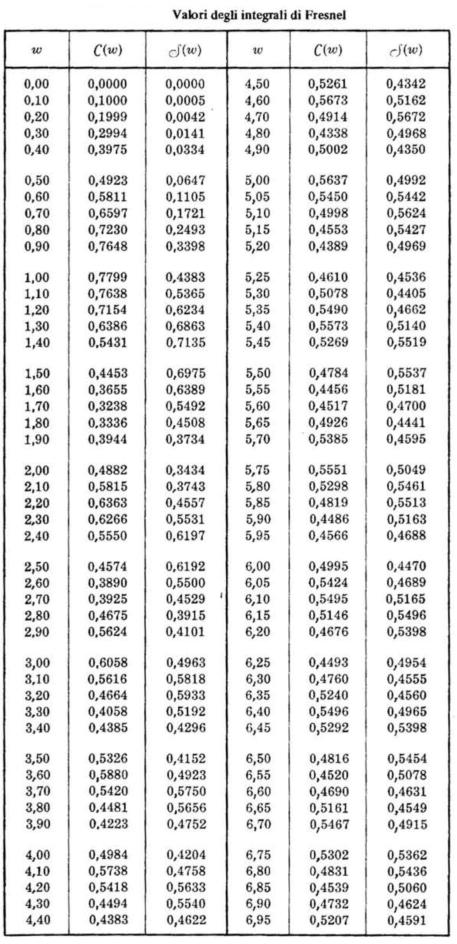
essere valutato in base agli integrali di Fresnel


dato che
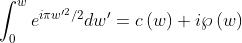
dove w sta sia per u che per v. Quindi concludendo

Si può dividere anche in questo caso il fronte d'onda in strisce e sommare quindi le
componenti del campo ottenendo ancora una spirale.
Alla stessa curva, detta spirale di Cornu e rappresentata nella sottostante figura, si
arriva riportando i punti

nel piano complesso per tutti i valori di w compresi tra
. A valori particolari
di , corrispondono i punti della spirale . Il vettore, o più
precisamente il fasore , ricavato da è il numero complesso dato da
, cioè

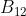
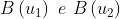
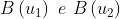



li campo elettrico in forma complessa nel caso specifico di una apertura rettangolare
è quindi

Dato che la lunghezza dell'elemento di arco della spirale è dato da ,
dalla definizione degli integrali di Fresnel segue che

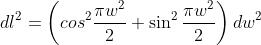
Quindi
corrisponde alla lunghezza dell'arco misurata lungo la spirale.


Si ricordi che per semplicità si è assunto che il fattore di obliquità sia uno e che le
ampiezze delle onde secondarie siano indipendenti da . Se non si fossero fatte
queste assunzioni, si sarebbe ottenuto una curva di vibrazione avvolta un po' più
strettamente della spirale di Cornu.
Dato però che , l'effetto è del tutto trascurabile.
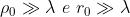
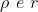

[1]
1)
Ricavare una espressione della intensità di radiazione nella figura di diffrazione su
campo vicino dovuta alla apertura rettangolare di figura [1], supponendo che le
onde incidenti siano piane.
Se le onde incidenti sono piane e quindi

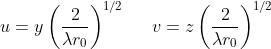
nella espressione di . L'espressione di può essere scritta in forma più esplicita



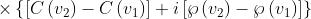
Dato che
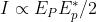


dove, nel caso di onda senza ostruzioni, .



2)
Una onda piana con di intensità di radiazione colpisce
normalmente uno schermo opaco in cui è praticato un foro quadrato di 4 mm
di lato.
Calcolare l'intensità di radiazione che si ha in un punto dell'asse posto a 4 m
dal centro del foro.


Riferendosi alla figura [1], gli spigoli dell'apertura sono definiti da
essendo l'origine del sistema di
riferimento sulla retta al centro della apertura. Quindi, essendo

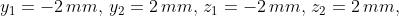
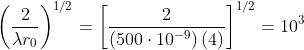
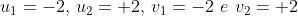
Gli integrali di Fresnel sono funzioni dispari; si ha cioè

Ne segue per il problema 1)

Dalla soprastante tabella, si ha che . Quindi
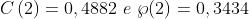


3)
Una onda piana con intensità di radiazione lo colpisce normalmente
una apertura quadrata di 2 mm di lato. A 4 m dallo schermo sulla perpendicolare
ad esso a 0,1 mm sulla sinistra del centro (direzione delle y negative) è collocata
una piccola sonda. (a) Determinare il valore della intensità di radiazione rilevato dalla
sonda. (b) Dimostrare che si ha lo stesso risultato anche 0,1 mm a destra dell'asse
centrale.

(a) La retta che passa per S e P è ora 0,1 mm a sinistra del centro dell'asse y.
Misurando le distanze dal punto O di intersezione della retta
col piano della
apertura, si ha Dato che

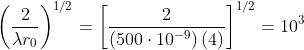


Dal problema 1)


oppure,utilizzndo la soprastante tabella


(b) A destra del centro,
Da cui e quindi


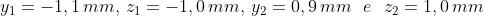

che è lo stesso risultato di (a).

4)
Applicare la rappresentazione tramite la spirale di Cornu
(a) al problema 2),
(b) al problema 3).
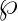
(a) Nel problema 2) si hanno
le coppie di variabili normali
ed anche
. Dato che
in questo caso le due coppie
sono eguali, .
Tuttavia in termini molto gene-
-rali per una apertura rettan-
-golare si ha
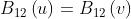


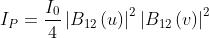
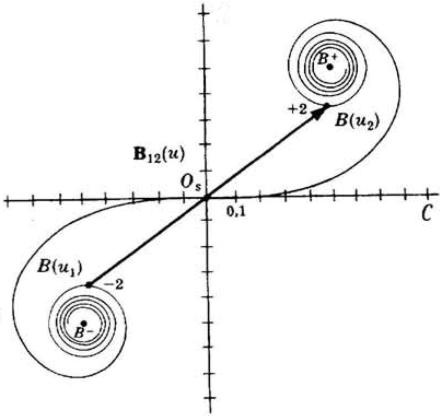
Per determinare basta
individuare e
unirli con un segmento di lun-
-ghezza , come nella
figura a lato.



Si misuri la lunghezza di con una scala
qualsiasi adatta allo scopo e si legga quindi il valore corrispondente sugli assi ;
in questo caso esso è circa 1,2 unità. Per una valutazione più precisa di



si parte da
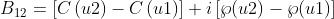
da cui

A causa della simmetria

(b) Si determina la posizione di e di
come indicato nella sottostante figura. La lunghezza di è circa 1,75, mentre
quella di è sempre approssimativamente 1,78. Quindi




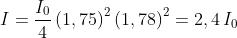



5)
Una sorgente puntiforme S di radiazioni monocromatiche aventi nel vuoto lunghezza
d'onda è collocata a 1 m di distanza da uno schermo piano opaco in
cui è praticata una lunga e stretta fenditura orizzontale di larghezza .
Determinare la intensità di radiazione risultante in un punto P posto sulla retta
che interseca perpendicolarmente l'asse della fenditura a 4 m dalla stessa, usando
la spirale di Cornu.


Per una apertura rettangolare
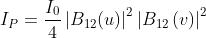
Nel caso di una fenditura lunga, e quindi .
I valori limiti di sono rispettivamente B+ e B- (riferendoci alla iniziale
figura [2]). Quindi nella direzione delle y si ha , che è eguale, in
base alla spirale di Cornu, a
. In altre parole, il segmento di retta che unisce
B- a B+, passando per O; cioè che va dal punto (-0,5, -0,5) al punto (0,5, 0,5),
è lungo unità. Quindi la espressione sopra riportata applicata al caso di una
fenditura stretta diventa


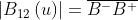

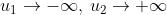
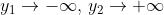
[2]

Inserendovi i valori numerici dati,
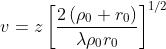
diventa
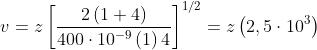
Essendo P sul piano perpendicolare alla fenditura e passante per la sua mezzeria,
,e quindi VI = -0,25, v2 = +0,25. La lunghezza
dell'arco compreso tra è ; quindi la corda è
leggermente minore di 0,5 e

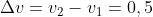
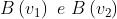



6)
Nel precedente problema, la fenditura era molto stretta e il sistema di frange
assomigliava ad un sistema di Fraunhofer.
Si supponga ora che essa sia larga 1,6 mm e si tracci il diagramma di I a parità
di altre condizioni.
Ancora una volta , ma ora , quindi
. La grandezza
è indipendente dala posizione di P,
a condizione che P sia sempre ad una distanza fissa dallo schermo. Si può equipararla
ad un tratto di filo appoggiato in cima alla spirale. Quando P si sposta verticalmente,
il tratto di filo scivola su o giù lungo la spirale, e quindi cambia la lunghezza del
segmento di retta che unisce le sue estremità. Invece di riportare in grafico I in
funzione di z, si riporti in funzione di , che è la posizione del
punto medio del tratto di filo.
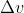

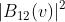






I risultati applicabili ad ogni caso di fenditura in cui
, sono riportati
nelle soprastanti tabella 1 e figura.
Questa dà il diagramma della intensità di radiazione che sarebbe rilevata da
una piccola sonda che si sposta verticalmente attraverso la fenditura. Ciò che
praticamente si osserverebbe, sarebbe una frangia centrale orizzontale grigia,
contornata sui due lati da zone luminose e scure disposte simmetricamente.


7)
Ricavare una espressione per l'intensità di radiazione in un punto posto oltre uno
schermo opaco piano semiinfinito e discutere la figura di diffrazione su campo vicino.
Si consideri anzitutto una fenditura orizzontale stretta ricavata su uno schermo
verticale, per la quale (v. il problema 5))
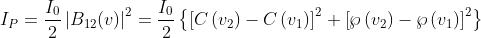
Si supponga ora di asportare la parte superiore dello schermo opaco lasciando uno
spigolo rettilineo.
Ne risulta che
, come anche
, e quindi , come pure .
Quindi
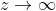
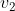
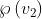
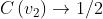

La sottostante figura [A], dà la grandezza di per cinque diverse posizioni di P
sulla verticale, dalla (l) più in basso
dello spigolo alla (5) ben sopra lo stesso. Invece la figura [B] dà i corrispondenti
valori della intensità di radiazione quali possono essere rilevati da una sonda che
si sposta verticalmente. Ovviamente le frange sono strisce orizzontali.
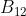

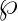

8)
Una lastra spessa di cartone opaco è disposta verticalmente in modo che il suo
bordo superiore sia orizzontale. Onde piane la colpiscono
normalmente. Calcolare l'intensità di radiazione in un punto posto a 2 m dallo
schermo e 0,8 mm sotto lo spigolo.

in base al precedente problema

dove

In questo caso
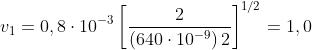
e quindi

ovvero


9)
Un raggio laser a He-Ne attraversa una lente positiva di 25 cm
di distanza focale. Un filo di 0,4 mm di diametro viene tenuto teso entro il raggio
in posizione verticale a 225 cm dalla lente e la figura di diffrazione su campo vicino
è raccolta su uno schermo posto a 3 m dal filo. Usare la spirale di Cornu per dete-
-rminare la intensità di radiazione in un punto centrale.


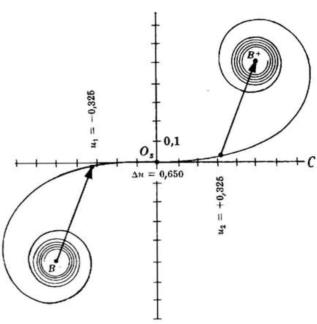

Visto da un punto centrale,
e . Quindi, essendo


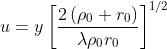
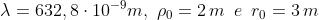
e

si ha
Quindi e la spirale a lato
mostra i due contributi al campo
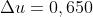

entrambi di lunghezza eguale circa a 0,51.
Quindi



Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





