



In un bacio, saprai tutto quello che è stato taciuto
OTTICA TEORICA

IL RETICOLO DI DIFFRAZIONE
FENDITURE SOTTILI MULTIPLE - IL RETICOLO DI DIFFRAZIONE
L'analisi condotta nei paragrafi precedenti per la diffrazione su campo lontano può
essere applicata anche ad un sistema di N fenditure. Se si considera la disposizione
geometrica della sottostante figura e il caso di onde piane normali al piano delle fenditure,
il campo in un generico punto P distante dallo stesso piano è



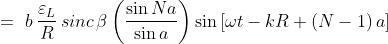
dove ancora una volta


Ne segue che la distribuzione della intensità di
radiazione su campo lontano nel caso di N
fenditure è data da
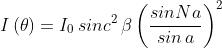
Nel punto , con cioè , la
densità di flusso dovuto a ogni singola
fenditura è e, come visto in un preceente
problema, trattando il caso del sistema lineare
di N emittenti, I(0) è eguale a .
La distribuzione della intensità di radiazione
che si ha in questo caso differisce da quella già vista solo perché ora si ha la modulazione
dovuta al fatto che le fenditure hanno una larghezza di valore finito.



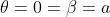

Per reticolo di diffrazione si intende qualsiasi disposizione periodica di elementi di
diffrazione, aperture od ostacoli, che alterano la ampiezza, la fase o entrambe di una
onda incidente. Il sistema di fenditure della soprastante figura, costituisce chiaramente un
reticolo di diffrazione, per quanto il sistema più comune sia quello costituito da varie
migliaia di solchi paralleli ricavati sulla superficie di una lastra di vetro.

1 )
Determinare la posizione dei massimi principali e secondari e la posizione dei minimi
nella figura su campo lontano prodotta da un sistema di N fenditure sottoposte ad
illuminazione normale monocromatica.
I massimi principali si hanno dove

cioè dove , o, esprimendosi in altro modo, dove
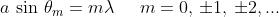
I minimi di densità di flusso si hanno dove
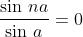
o dove
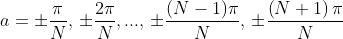
I valori di a mancanti dall'elenco, , corrispondono a picchi
anziché a zeri. Tra due massimi principali consecutivi ci sono N-1 minimi e quindi
N-2 massimi secondari. Questi si trovano pressappoco a mezza strada tra gli zeri in


In realtà essi si trovano leggermente spostati verso il massimo principale più vicino.

2)
Ricavare una espressione approssimata delle in tensità di radiazione relative ai primi
tre massimi secondari nella figura monocromatica di Fraunhofer di N fenditure con N
molto grande.
Per il precedente problema, i massimi secondari si trovano, con buona approssima-
-zione, dove


Dato che

Nei punti che si considerano ora . Inoltre, avendo assunto che N sia
grande, i valori di a per i primi massimi secondari fino ad un certo numero sono piccoli,
per cui si può porre
.
Anche i valori di sono piccoli e quindi assume valori molto vicini a 1. Allora
nel primo massimo secondario
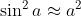
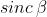

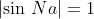
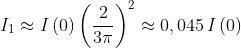
o
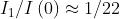
L'intensità di radiazione nel secondo massimo è


o

E nel terzo massimo o


3)
Tracciare un disegno approssimato della immagine di diffrazione su campo lontano
dovuta a un sistema di 6 fenditure parallele distanti l'una dall'altra di un tratto
eguale a 4 volte la larghezza da ogni singola fenditura. Determinare la intensità di
radiazione relativa al secondo massimo secondario adiacente al primo massimo
principale.
Dato che a = 4b, ci si deve aspettare che il 4° ,8°, 12°, ecc. massimo principale
siano assenti e sostituiti da valori nulli della intensità di radiazione. Inoltre tra due
massimi principali consecutivi ci saranno N-2= 4 massimi secondari e questi avranno
valori piuttosto piccoli; quanto piccoli lo si può determinare con la relazione

Il secondo massimo secondario corrisponde approssimativamente a

Ma
, il che significa che
e quindi

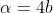

Ne segue che l'intensità di radiazione in questione è

La seguente figura dà l'andamento della figura di diffrazione in esame.


4)
Generalmente la sorgente usata nei dispositivi spettroscopici per illuminare un
reticolo consiste di una fenditura stretta e quindi i massimi principali si presentano
come strisce
luminose sottili (donde il nome di righe spettrali). Dimostrare che
nel caso di luce rnonocromatica a incidenza normale, la larghezza angolare
di
una riga di questo genere è inversamente proporzionale alla larghezza del reticolo.

Si assuma che un massimo principale si estenda per il tratto compreso tra i due
minimi adiacenti, cioè da , come nel problema 1).
La larghezza del massimo è quindi


Ma , per cui
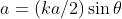
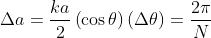
Quindi la larghezza angolare della riga spettrale di ordine m è
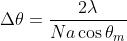
che varia in modo inversamente proporzionale con Na, la larghezza del reticolo.
Questa relazione è nota come allargamento strumentale. Maggiore il numero dei
solchi e maggiore la loro distanza, più strette risultano le righe spettrali.
Dato che N è grande, i massimi secondari hanno intensità di radiazione di valore
estremamente piccolo per cui in pratica "si vedono" solo i massimi principali.

5)
(a) Ricavare una espressione che dia l'ampiezza angolare per un intervallo piccolo
di lunghezza d'onda, , cioè la dispersione angolare o il potere
dispersivo
.
(b) Determinare il potere dispersivo nel primo e nel secondo ordine per un reticolo
con 1500 solchi ogni pollice e operante nel campo del visibile.
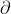

(a) Si sa già (v. problema 1) che i massimi principali si hanno per

relazione detta equazione del reticolo per incidenza normale. Quando il reticolo è
illuminato con luce bianca ogni lunghezza d'onda ha evidentemente un massimo
di un dato ordine in una posizione corrispondente ad un valore di
leggermente
diverso da quello di un'altra lunghezza d'onda.
Da questo fatto risulta una ampia banda di colori o spettro per ogni valore di m
(vedi sottostante figura).
Derivando la equazione del reticolo si ha
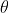

(b) La distanza tra solco e solco o costante del reticolo è data, in centimetri, da
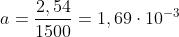
che rappresenta un valore molto elevato in confronto a
In base alla equazione del reticolo è evidente che nel primo e nel secondo
ordine, essendo . Quindi i poteri dispersivi sono rispet-
-tivamente
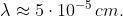
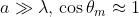
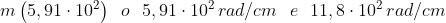


6)
Determinare la distanza angolare tra le righe D del sodio (589,592 nm e 588,995
nm) nello spettro del primo ordine prodotto da un reticolo piano a trasmissione
avente 10.000 tratti per pollice e sottoposto ad illuminazione normale.
La differenza tra le lunghezze d'onda è abbastanza piccola per cui
si può usare la equazione


ottenuta nel precedente problema. Questa volta
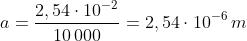
e quindi dalla equazione del reticolo con m = 1,

Quindi . Infine
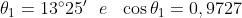
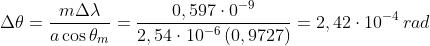

7)
Determinare la ampiezza angolare dello spettro del primo ordine della luce bianca
(da 390 nm a 780 nm) che illumina normalmente un reticolo a trasmissione con
17 000 solchi per pollice.
L'intervallo delle lunghezze d'onda in questione è troppo ampio perché si possa
usare la equazione ricavata per
. Si calcolano invece gli angoli direttamente,
usando la equazione del reticolo con m = 1, cioè
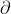
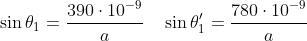
Calcolando a si ottiene

Di conseguenza,

da cui


8)
Il potere risolutivo cromatico
di un dispositivo spettroscopico è per definizione
dove
è la lunghezza d'onda media e corrisponde alla minima differenza
tra lunghezze d'onda risolvibile tra due righe adiacenti. Come criterio di risolubilità si
adotta il criterio di Rayleigh che stabilisce che due frange adiacenti arrivano giusto ad
essere risolubili quando il massimo principale di una coincide con il primo minimo
dell'altra. Ricavare una espressione per il potere risolutivo di un reticolo.

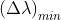
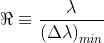
In base al criterio di Rayleigh si può dire che la distanza angolare minima tra due
massimi alla soglia inferiore di risolubilità corrisponde alla metà della larghezza di
un massimo principale. Dal problema 4) e quindi
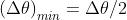

Ma dal problema 5)

Combinando le due espressioni si ha
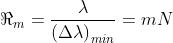
per il potere risolutivo corrispondente all'ordine m-esimo.

9)
Quanti solchi si devono tracciare su un reticolo a trasmissione se si vuole che esso
arrivi giusto a risolvere il doppietto del sodio (589,592 nm e 588,995 nm) nello
spettro del primo ordine?
In base al precedente problema, il potere risolutivo di un reticolo nel primo ordine è

In questo caso


Quindi
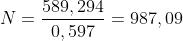
e quindi occorrono 988 solchi


10)
Nei reticoli moderni i solchi sono sagomati, allo scopo
di trasferire la maggior parte dell'energia al di fuori
dell'ordine zero dove essa è sprecata da un punto di
vista spettroscopico perché le varie lunghezze d'onda
si sovrappongono. In figura a lato è dato un reticolo
a riflessione sagomato che sposta il picco forte riflesso
specularmente dall'ordine zero a un ordine superiore.
(a) Ricavare una espressione che dia l'ordine rinforzato
in funzione dell'angolo di sagomatura y riferendosi al
caso di onde piane che colpiscono normalmen te il
piano del reticolo.
(b) Calcolare quale deve essere l'angolo y affinché
l'energia raggiante di lunghezza d'onda 200 nm che
colpisce normalmente il reticolo sia fortemente
concentrata nel secondo ordine essendo il reticolo di
2000 tratti/mm
(a) Se le facce del reticolo di figura non fossero inclinate, la riflessione speculare
concentrerebbe la maggior parte dell'energia in nell'ordine zero; invece ora essa
esce con inclinazione Si noti che
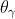
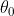

dove è un numero negativo dato che rispetto alla normale al reticolo si trova dalla
stessa parte di Nel caso di incidenza normale , l'ordine zero (m=0) si ha
per , cioè sulla normale al piano del reticolo. La maggior parte della radiazione
diffratta è ora concentrata in e questa direzione corrisponde all'ordine
m-esimo quando
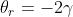



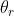

In questo caso il picco di interferenza di ordine m si viene a trovare sul massimo
centrale della figura di diffrazione dovuta a una sola fenditura.
(b) Dato che

da (a) si ha


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





