



Non piangere perché è finito, sorridi perché è successo
OTTICA TEORICA
COERENZA

Il concetto di sorgente puntiforme monocromatica è una astrazione matematica.
Le migliori sorgenti reali emettono onde di lunghezze comprese in un certo intervallo, per
quanto stretto.
Come si vedrà nelle seguenti pagine, il solo fatto che una emittente non sia stata accesa
per sempre significa che il suo segnale deve essere policromatico.
Si può anche immaginare la emissione come composta da treni d'onda finiti, invece che
da una sinusoide con una sola frequenza ed infinitamente lunga.
Nella sottostante figura (b) è rappresentato il campo di un'onda reale.
L'intervallo di tempo durante il quale la fase resta abbastanza costante è detto tempo di
coerenza
, un concetto che è già stato introdotto.
Il corrispondente intervallo spaziale
è detto lunghezza di coerenza.
Si noti che per un'onda monocromatica è infinito ma
è nullo. Quando diminuisce,
la larghezza della banda di frequenze su cui l'emittente irradia aumenta e tra i rispettivi
ordini di grandezza vale la relazione

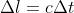
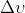


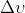

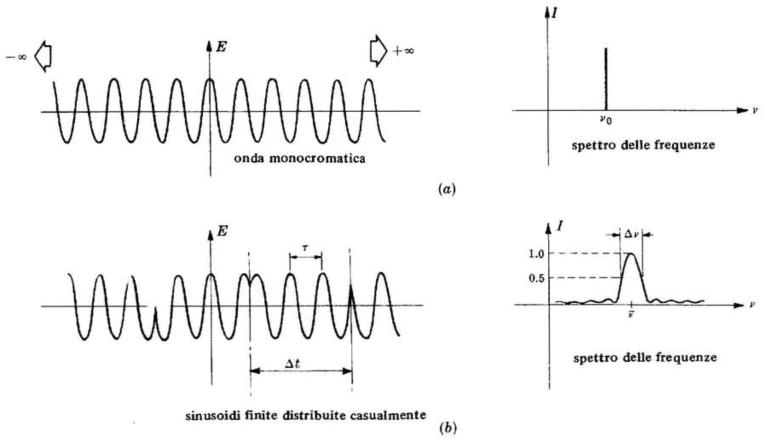
Quando lo spettro delle frequenze si allarga, la lunghezza del treno d'onda nello spazio
come pure il tempo di coerenza diminuiscono e si dice che si ha una diminuzione della
coerenza longitudinale o temporale.
Si supponga ora di avere una sorgente puntiforme
di luce quasi monocromatica S (vedi figura a lato).
E' evidente che tra i campi elettrici in P1 e P2 esiste
una relazione se , cioè quando un singolo
treno d'onda può facilmente abbracciare la distanza
tra i due punti.
Allo stesso modo è evidente che tra i due campi non deve sussistere alcuna relazione
quando , dato che in qualsiasi istante si avranno in P1 e P2 treni d'onda
differenti.
Data una sorgente, il grado di correlazione che sussiste tra i campi variabili nel tempo
è un indice del suo grado di coerenza temporale.



Se la sorgente fosse una sorgente puntiforme perfetta, i campi in P1 e P3 sarebbero
identici, cioè totalmente correlati. Ma se la sorgente si allarga, la correlazione diminu-
-isce e si parla di diminuzione della coerenza spaziale laterale.
La visibilità
delle frange prodotte da un interferometro (precedentemente visto) è, in
termini molto generali, una misura del grado di coerenza. Ne segue che spostando in un
interferometro di Michelson lo specchio, si può studiare la coerenza temporale e che,
variando la distanza tra i fori di un apparato di Young, si può studiare la coerenza
spaziale.
Si supponga, ad esempio, che P1 e P3 della soprastante figura, corrispondano ai due
fori di spillo S1 e S2 dell'apparato di Young (già visto). Dato che ogni sorgente reale ha
dimensioni finite, si supponga che S abbia la forma di un disco di diametro D che a
distanza R dal piano dell'apertura sottenda un angolo .
Variando la distanza a tra S1 e S2, si può dimostrare che le frange di interferenza
spariranno (si ha cioè il primo valore nullo di quando , dove





e è la lunghezza d'onda media della sorgente quasi monocromatica. Una "buona
coerenza" con visibilità 0,88 o superiore si ha quando

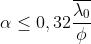
La visibilità cade di fatto dal suo valore massimo fino a zero e poi continua a oscillare
tra massimi secondari, molto piccoli e sempre decrescenti, e zero.
La distribuzione della intensità di radiazione nell'esperimento di Young è, come si
può dimostrare,

In questo caso è il grado complesso di coerenza, il cui valore assoluto è legato
alla coerenza in P nel modo seguente

coerenza limite

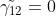

non-coerenza limite
coerenza parziale
La variabile
è la differenza tra i tempi . La intensità di radiazione
può essere espressa anche in una forma ancora più simile a quella descritta in un
precedente paragrafo :
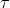
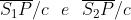

Si noti che allora si era assunto che S fosse una sorgente puntifonne
monocromatica, il che implica la coerenza limite .


1 )
Determinare la larghezza della banda di frequenze per la luce bianca. Determinare
lunghezza di coerenza e tempo di coerenza relativi.
In base alla tabella specificata nelle precedenti pagine, sappiamo che la luce bianca
va da 384 THz a 769 THz, per cui la larghezza della banda di frequenza è
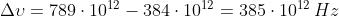
La relazione tra
,
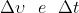

porta ad un tempo di coerenza , e a una lunghezza di coerenza
. Si osservi che i treni d'onda della luce bianca hanno all'incirca la
lunghezza di una lunghezza d'onda.

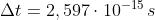

2)
La purezza spettrale di una sorgente può essere valutata tramite la grandezza
, detta stabilità di frequenza. Una lampada all'isotopo a bassa
pressione ad esempio, presenta una banda di frequenze
di larghezza
. Determinare la lunghezza e il tempo di coerenza di
questa luce e la sua stabilità di frequenza.


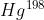

Il tempo di coerenza è . La lunghezza di coerenza , è
uguale a 29,9 cm. La lunghezza d'onda media è data; quindi dato che
è piccola,
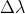

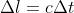

Infine la stabilità di frequenza è
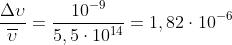
ovvero circa 2 parti per milione

3)
Ricavare una espressione che dia la lunghezza di coerenza di un'onda in funzione
della larghezza della riga corrispondente ad una larghezza della banda di
frequenze di
.
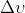
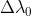
La velocità dell'onda nel vuoto è . Quindi e derivando si ha



Il segno meno sta solo ad indicare che la variazione' di
avviene in senso opposto
a quella di . Trascurando il segno e usando la relazione
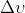
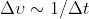
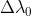
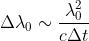
o, dato che
,
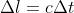
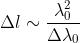

4)
Un interferometro di Michelson è illuminato con la luce rossa di una lampada al
cadmio di lunghezza d'onda media 643,857 nm e una larghezza di riga di 0,0013 nm.
La disposizione iniziale corrisponde a una O.P.D. nulla, cioè a d=0. Poi si sposta
adagio uno specchio fino a far sparire le frange di interferenza.
Di quanto bisogna spostarlo?
A quante lunghezze d'onda corrisponde questo spostamento?
Lo spostamento d che bisogna dare allo specchio è connesso alla lunghezza di
coerenza e quindi alla larghezza della riga. Anzitutto si calcola quindi
da è

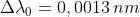

Quando la O.P.D., che è eguale a 2d, supera
le frange devono svanire; quindi

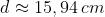
Ciò equivale a onde.
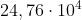

5)
Si supponga di ripetere l'esperimento del precedente problema con luce
prodotta da un laser a He-Ne con stabilità di frequenza di
2 parti per
.
Di quanto va spostato in questo caso lo specchio per ottenere che le frange di
interferenza scompaiano?
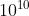

Si sa che

Quindi
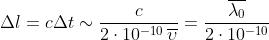
Sostituendo il valore di
si ottiene M - 3164 m. Ne segue
e
(Sarebbe un interferometro piuttosto lungo!)




6)
Si supponga che in un apparato di Young l'illuminazione sia fornita da una sorgente
quasi monocromatica S formata da una lampada a scarica posta
dietro un foro circolare di 0,1mm di diametro praticato in uno schermo.
Qual è la distanza
tra i due fori necessaria perché le frange di interferenza
scompaiano se la distanza tra S e il piano dei due fori è di 2 m?

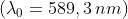
La visibilità dovuta ad una sorgente circolare diventa nulla quando
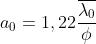
dove
è l'angolo sotteso dalla sorgente estesa. Questo angolo è approssimativa-
-mente eguale al rapporto tra il diametro della sorgente e la sua distanza da , cioè

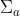

Quindi
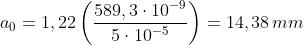
Si noti che se si allontana da S, se cioè R cresce,
aumenta. Ciò implica che
se ci si allontana abbastanza anche dalla sorgente più grande che si voglia
immaginare, ad es. una stella, diventa una grandezza misurabile.


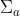

7)
Si supponga che il diametro del Sole sottenda sulla superficie terrestre un angolo di
½° e si determini l'area di coerenza, vale a dire l'area circolare nella quale si può
praticare un gruppo di aperture ottenendo delle frange di interferenza ben distinte.
Si consideri una lunghezza d'onda media di 550 nm.
L'area di "buona coerenza" può essere evidentemente espressa come
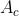

In radianti e quindi
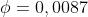


8)
La sottostante figura rappresenta una sorgente lineare quasi monocromatica S
che illumina un apparato di Young. Ricavare una espressione per
, la distanza tra
i fori che dà il primo caso di
(ossia per la quale le frange scompaiono per
la prima volta).

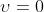

Si considerino le onde che provengono dai punti indipendenti S1 e S2 alle due
estremità di S. Le frange coseno che derivano indipendentemente da S1 e S2
sono centrate rispettivamente in su .
Il valore di questi angoli è approssimativamente dato da
a condizione che . Il sistema di frange di interferenza scompare la prima
volta quando il primo minimo di una figura si sovrappone al massimo centrale
dell'altra. Come già si è visto , la prima coppia di minimi si ha a distanze
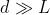

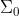
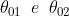
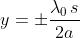
dal centro, o, essendo y/s=0, essi sono visti da S1 con gli angoli

La distanza tra frange è molto grande quando a è molto piccola e al crescere di a il
primo minimo di S1 si sposta verso il massimo di ordine zero di S2 finché si
sovrappongono per , dove


Quindi
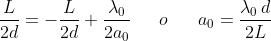

9)
Ricavare una espressione che dia la visibilità in un esperimento di Young in funzione
del grado di coerenza , cioè del valore assoluto del grado complesso di coerenza
(Il piccolo tilde sopra
sta solo a ricordare che si tratta di una grandezza
complessa).
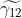
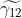

La visibilità

può essere determinata usando la formula

Quindi


e
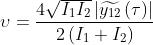
Si osservi che quando , si ha , per cui la visibilità delle frange è una
misura diretta della coerenza delle onde.




Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





