



Anche quando si inveisce contro di me, guadagno rinomanza
OTTICA TEORICA
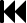
INTERFEROMETRI A DIVISIONE DI AMPIEZZA

Nei numerosi dispositivi a film sottili finora esaminati le due onde coincidevano per la
maggior parte del percorso tra S e P. Adesso si tratteranno gli interferometri a divisione
di ampiezza che, con l'uso di specchi aggiuntivi, separano le due onde in modo che
esse possono essere manipolate individualmente prima di essere ricombinate.
L'interferometro di Michelson (1881) riportato nella sottostante figura è rappresentativo
di questa classe piuttosto ampia di dispositivi ed è contemporaneamente uno degli stru-
-menti ottici più importanti, per lo meno da un punto di vista storico
Come si vede dalla figura, la luce proveniente da una sorgente estesa colpisce il divisore
d'onda ed è divisa in due onde di ampiezza diversa. Una è riflessa dallo specchio M2,
passa attraverso il divisore d'onda B e arriva al rivelatore. L'altra è dapprima riflessa dallo
specchio M1 quindi dal divisore d'onda e arriva al rivelatore. La lastra del compensatore è
identica per spessore e orientamento al divisore d'onda. La sua funzione è quella di rendere
eguali le lunghezze di cammino ottico quando M1 e M2 sono alla stessa distanza da B.
In altre parole le due onde attraversano lo stesso spessore di vetro, come indicato nella
figura che segue.
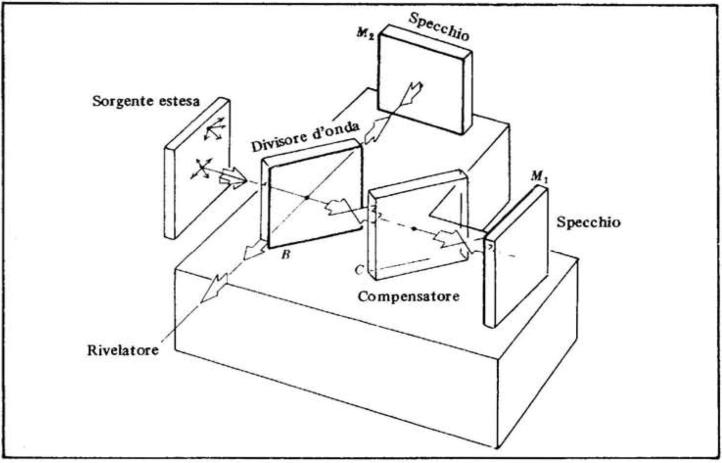
In effetti lo spazio compreso tra M2 e M’1,
immagine di M1 nel divisore d'onda, funziona
come un film d'aria sostanzialmente come
quelli visti nellla precedente pagina.
Ne segue che quando M2 e M1 sono esat-
-tamente perpendicolari l'uno all'altro, il film
di aria racchiuso è piano e ha spessore d.
La figura di interferenza consiste di una serie
di frange circolari concentriche di eguale
inclinazione.
Si possono considerare due sorgenti virtuali,
immagini di S, poste sull'asse ottico che passa
per M2 e M1’. Esse producono frange, inoltre
quando M2 e M1’ sono vicini e inclinati
l'uno rispetto all'altro, il film di aria che essi
[Fig. A]
racchiudono è un cuneo sottile e produce
frange a linee rette parallele .
Si tenga presente che la riflessione interna ed esterna sul divisore d'onda produce uno
sfasamento angolare tra le due onde. La grandezza dello sfasamento dipende dalla natura
delle interfacce. Qui si supporrà che il divisore d'onda sia una lastra di vetro, nel qual caso
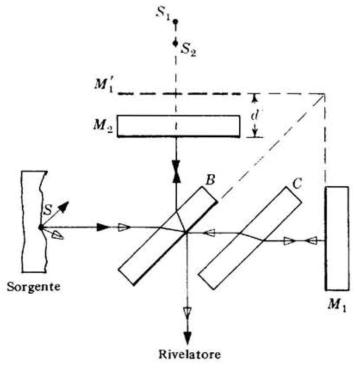
lo sfasamento è di
radianti.


1 )
In un interferometro di Michelson gli specchi sono disposti in modo tale che guardando
dentro il divisore d'onda si vede un campo luminoso di 3 x 3 cm corrispondente alla
zona di sovrapposizione della vista dei due specchi M1 e M2. Se la luce è di 600 nm
il campo luminoso mostra 24 frange luminose verticali. Calcolare di quanto si scostano
dalla perpendicolarità i piani degli specchi Ml e M2.
Per un precedente problema, la distanza tra frange nel caso di cuneo sottile può essere
espressa come .
Ma in base ai dati si ha


Ciò significa che


2)
In un interferometro di Michelson, uno dei due specchi, ad esempio M1, generalmente
è mobile. Si supponga che il dispositivo sia messo a punto per dare frange circolari e
si sposti quindi lentamente M1 in modo che M’1 si accosti a M2, cioè diminuisca d.
Le frange si spostano verso il centro del campo; si supponga in particolare che quando
si sposta M1 di m scorrano davanti 850 frange luminose. Si supponga che
il dispositivo sia illuminato da luce quasi monocromatica e si determini la sua lunghezza
d’onda.
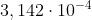
Ritornando ad un precedente problema, si può dimostrare che se lo spessore del film
piano cresce di , l'ordine m cresce di uno. In altre parole, O.P.D. cresce di
quando d cresce di , dato che l'onda attraversa il film due volte. Quindi 850
frange luminose corrispondono ad uno spostamento dello specchio di
ossia
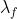




e perciò
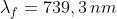

3)
Si consideri un interferometro di Michelson illuminato da una sorgente che emette
un doppietto di lunghezze d'onda (riferite al vuoto), . Man mano che si
sposta uno degli specchi, le frange compaiono e scompaiono periodicamente.
Si supponga che lo spostamento di uno specchio provochi un ciclo completo di
variazione della visibilità e si ricavi una espressione di in funzione di
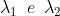



Le frange saranno nettamente visibili quando le bande luminose di '" pressappoco si
sovrappongono alle bande luminose di mentre invece la visibilità dell'interferenza
sarà minima quando le bande luminose di si sovrappongono alle bande scure di
Quest'ultima situazione si verifica quando la O.P.D. è un multiplo intero di e
contemporaneamente un multiplo secondo un numero dispari della metà di
Quindi





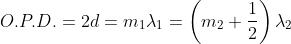
è la condizione di visibilità minima. Quindi

e sottraendo si ha

Il numero intero cresce di una unità quando d diventa cioè al
successivo verificarsi della condizione di visibilità minima. Si ha quindi



Sottraendo le ultime due equazioni si ha


4)
Una lastra sottile trasparente di indice n e spessore L è disposta perpendicolarmente
all'asse del raggio luminoso in uno dei bracci di un interferometro di Michelson.
Determinare di quanto deve essere spostato lo specchio di quel braccio quando si
toglie la lastra se si vuole avere lo stesso numero di frange osservato prima della
rimozione.
Inserendo la lastra si varia la lunghezza del cammino ottico in quella zona da IL per
l'aria a nL e quindi la variazione di O.P.D. prodotta dai due attraversamentì della
lastra è 2(n - I)L. Se lo spostamento dello specchio deve compensare l'assenza
della lastra, esso deve produrre una eguale
.
Quindi




5)
In uno dei bracci di un interferometro di Michelsonè inserita perpendicolarmente una
lamina sottile di fluorite (CaF2) di indice 1,434. Quando si illumina con ,
si osservano 35 frange. Determinare lo spessore della lamina.

Come visto nel precedenten problema e, in questo caso, .
Ne segue



da cui


6)
Guardando in un interferometro di Michelson si vede un disco scuro centrale
circondato da anelli luminosi e anelli scuri concentrici. Un braccio del dispositivo è
2 cm più lungo dell'altro e . Determinare (a) l'ordine del disco centrale,
(b) l'ordine del sesto anello scuro.

(a) Nei precedenti paragrafi si è visto che per frange di eguale inclinazione con uno
sfasamento da riflessione di
radianti


I minimi corrispondono a quegli angoli per i quali ; cioè



In questa formula m è l'ordine della frangia scura che sottende il mezzo angolo .
Ciò può coincidere o no con l'ordine che si trova contando le frange. Per distinguere
i due tipi di ordini, si indica con l'ordine della frangia scura il cui ordine nella
successione è j. Il disco centrale ha quindi ordine , per cui la formula
sopra data si semplifica e diventa



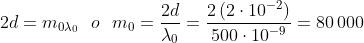
(b) Il p-esimo anello scuro (non contando il disco) ha ordine , dato che
ogni minimo successivo sta ad indicare una O.P.D. diminuita di una lunghezza
d'onda. In particolare ciò significa che l'ordine del sesto anello
è

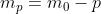


7)
L'interferometro di Jamin (1856),illustrato nella sottostante figura, consiste di due
lastre di vetro piane e spesse (-2,5 cm) identiche, rese opache su un lato argentato.
La sorgente luminosa è estesa e la luce arriva a circa 45°.
(a) Discutere la figura che si ottiene quando le lastre sono perfettamente parallele
l'una all'altra. Le onde che interferiscono hanno ampiezze quasi eguali o molto
diverse?
(b) Descrivere le frange che si hanno quando le due lastre vengono ruotate a
formare un cuneo sottile il cui spigolo di punta sia parallelo alla linea
tratteggiata (
)


(a) Si considerino le due lastre parallele e il raggio incidente in A. L'onda subisce
una divisione di ampiezza, e la frazione più debole viene riflessa fino al punto F.
Ma anche la riflessione in D è debole e le due onde, avendo seguito rispettivamente i
percorsi SAFED e SABCD, escono con ampiezze eguali. Esse sono anche in fase perché
hanno percorso cammini e subito riflessioni equivalenti e quindi si sovrappongono e
interferiscono costruttivamente.
Ciò avviene per tutti i raggi, per cui il campo di osservazione è uniformemente luminoso.
(b) Quando si ruotano le lastre formando un cuneo, si può considerare detta figura
come una sezione trasversale in un piano orizzontale. Tutti i raggi paralleli a SA, in
qualsivoglia di tali piani orizzontali, arriveranno allo stesso punto centrale, formando
una macchia luminosa sul piano dell'immagine della lente. Qualsiasi altro raggio oriz-
-zontale che entra con una data inclinazione dà luogo ancora ad interferenza costruttiva
e tutti i raggi di questo tipo in tutti i piani orizzontali arrivano in una serie di punti che
formano una linea luminosa orizzontale - il massimo di ordine zero.
Nel caso di raggi non orizzontali invece, le due porzioni dell'onda subiscono uno
sfasamento.
Il risultato finale è una serie di frange luminose e scure egualmente distanziate ed
orizzontali.

8)
Si supponga di introdurre in un interferometro di Jamin due celle trasparenti identiche,
come nella sottostante figura. Le due celle, delimitate da piani ottici, sono lunghe
23 cm e contengono entrambe argo di indice di rifrazione 1,000281. Quando il
dispositivo è illuminato con luce al sodio compare un sistema di frange
e la figura di interferenza cambia non appena si aspira il gas dalle camere. Quante
frange luminose attraverseranno una linea segnata da un capello messo di traverso
sul telescopio ?
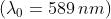

Una frangia passa davanti ad una data linea di riferimento ogni volta che la O.P.D.
varia di una lunghezza d'onda.
Per una cella di lunghezza L la variazione di O.P.D. è

e il numero N di frange a cui ciò corrisponde è


9)
L’interferometro di Twyman-Green (1916) della sottostante figura è diventato uno
strumento di grande valore per la verifica di elementi ottici. La prova si esegue
sostituendo allo specchio M2 l'elemento da esaminare e uno specchio addizionale tale
che, se l'elemento è perfetto, la combinazione dei due equivalga allo specchio sostituito
M2. Descrivere come funziona questo dispositivo nel caso di luce quasi monocromatica
e spiegare in che cosa differisce dal dispositivo di Michelson.
Spiegare come può essere usato per trovare una lente, un prisma e un piano ottico.

La caratteristica distintiva del sistema di Twyman-Green è l'uso di luce collimata.
Quando l'interferometro di Michelson è regolato in modo da avere un film piano di
aria tra M1 e M2 (v. soprastante fig [A]) si forma una figura ad anelli concentrici
perché la luce provenendo da una sorgente estesa contribuisce secondo la funzione
o in tutte le direzioni. Invece la luce collimata del dispositivo di Twyman-Green
illuminato a pari condizioni genera un campo uniformemente illuminato.
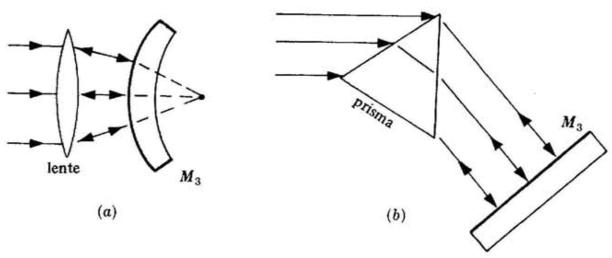
Si supponga ora di sostituire M2 con una lente in prova L e uno specchio sferico
perfetto M3 il cui centro coincida con il fuoco della lente, come nella sottostante
figura (a). Le onde piane attraversano la lente, sono riflesse dallo specchio ed escono
come onde piane se la lente in esame è perfetta. Se il fronte d'onda non è invece
piano, ciò significa che l'elemento non è perfetto e la cosa si nota chiaramente
dalla figura di interferenza.
Per studiare un prisma si può seguire il procedimento illustrato in figura(b), mentre
per un piano ottico basta inserirlo in uno qualsiasi dei bracci del dispositivo per
mettere in luce i suoi eventuali difetti.
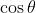



Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





