



Non dire mai alle persone più di quanto hanno bisogno di sapere
OTTICA TEORICA

INTERFEROMETRI DIVISORI DEL FRONTE D’ONDA

Come si è visto nelle precedenti pagine, si può assumere che una sorgente ordinaria di luce
emetta un gran numero di treni di onde quasi sinusoidali non correlati tra loro e ognuno di
durata eguale a circa
L'onda luminosa che ne risulta mantiene fase costante per un
intervallo di tempo un po' inferiore a questo tempo di coerenza,
Le onde che provengono
da due sorgenti del genere possono interferire, ma la relativa figura di interferenza avrebbe
una durata inferiore a
Dato che la fase delle onde cambia rapidamente ed a caso, anche la figura di interferenza
varia in modo casuale, cancellandosi nell'intervallo relativamente lungo del tempo di
osservazione.
Benché due laser a fase bloccata possano dare figure di interferenza rilevabili, il procedi-
-mento più seguito è quello di dividere una singola onda in due parti coerenti.
In senso lato, per interferometro si intende un qualsiasi dispositivo che genera frange di
interferenza. La sottoclasse degli interferometri a divisione del fronte d'onda sono
caratterizzati dal fatto che si portano due distinte frazioni di un'onda ad interferire
dopo aver fatto loro percorrere cammini ottici diversi.

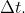
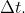

Gli interferometri a divisione del fronte d'onda, che sono di molti tipi diversi, sono
probabilmente illustrati nel modo più chiaro dal dispositivo della soprastante figura, detto
apparato di Young.
Le sorgenti sono o piccoli fori o fenditure molto strette e lunghe
perpendicolari al piano del disegno. L'onda che parte da
arriva in che a loro volta
funzionano come una coppia di emittenti coerenti ed in fase.
Per qualsiasi punto P distante dal piano delle fenditure e non lontano dall'asse centrale, la
differenza di lunghezza dei cammini ottici è . Essa è appros-
-simativamente eguale a o, più semplicemente, a
.
Dato che quando y è piccolo in confronto ad s,


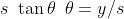


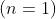
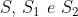

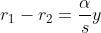
Le due onde arrivano in P in fase e interferiscono costruttivamente quando
dove Quindi i massimi di interferenza si hanno per



e il piano di osservazione è coperto alternativamente da frange luminose e frange
scure parallele tra loro, perpendicolari al piano del disegno. La regione compresa tra
è riempita di figure di interferenza


1 )
Ricavare una espressione che dia la distribuzione della intensità di radiazione sul
piano di osservazione nell'esperimento di Young e tracciare il grafico di I in funzione
di y.
Dato che le onde sono emesse da in fase, la differenza di fase che si ha in
P è semplicemente
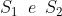

Da un precedente problema, si ha che
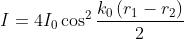
e dato che si ha


L'andamento risultante è riportato nel sottostante grafico


2)
Ricavare una espressione che dia la distanza tra due frange consecutive (cioè la
distanza tra due massimi o minimi consecutivi) nell’esperimento Young

I massimi m-esimo e (m + l)-esimo sono situati nelle posizioni

Ne segue che
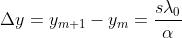
come può essere facilmente verificato nella soprastante figura

3)
Usare il formalismo dell'onda piana per verificare che le due onde che arrivano nel
punto p vicino all'asse centrale nell'esperimento di Young sono sfasate di .


La soprastante figura mostra i due versori di propagazione
e il vettore r che dà la posizione del punto P rispetto all'origine dell'asse centrale.
Le due perturbazioni che arrivano in P sono rappresentate dalle espressioni
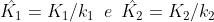


dove si è assunto Ne segue che
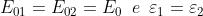

Ora si determina Dato che e che è un angolo molto piccolo





inoltre ; per cui
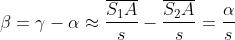
Perciò e

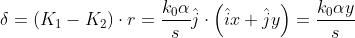

4)
Un raggio quasi monocromatico di lunghezza d'onda illumina un apparato di
Young generando una figura di interferenza in cui le bande scure consecutive sono
a distanza di 5,6 mm l'una dall'altra. Se la distanza tra il piano che contiene le
aperture, , e il piano di osservazione , è di 10m e se le sorgenti S1 e S2 sono
distanti 1,0 mm l'una dall'altra, qual è la lunghezza d'onda della luce?
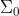


Dal problema 2) si ha che la distanza tra due bande consecutive è
Per cui


5)
In un apparato di Young, davanti ad una delle sorgenti secondarie è disposta una
cella di vetro lunga 25 mm e piena d'aria. L'aria viene quindi risucchiata e al suo
posto viene iniettato un gas da esaminare. Confrontando la figura di interferenza
nel caso dell'aria con quella che si ottiene con il gas, si osserva che tutta la figura
di interferenza raccolta sul piano si sposta di 21 bande luminose verso il lato
dove è collocata la cella. Dato che l'illuminazione è fatta con la riga rossa di
Fraunhofer C , il cui indice di rifrazione nell'aria è ,
qual è l'indice di rifrazione del gas?


La lunghezza del cammino ottico sul lato dove c'è la cella, quando questa è piena di
aria è quando è piena di gas è Quindi la differenza delle
lunghezze dei cammini ottici (O.P.D. - Optical Path-length Difference) è data da

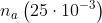
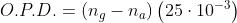
Ma essa deve essere eguale a 21 lunghezze d'onda; deve cioè essere
Ne segue che


da cui
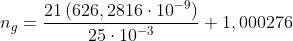
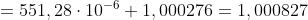

6)
Il doppio specchio di Fresnel consiste di due superfici speculari che formano tra di
loro un piccolo angolo
. Il dispositivo è illustrato nella sottostante figura. Spiegare
come funziona il sistema e ricavare una espressione di in funzione di la
distanza tra le bande e la distanza d.
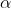
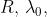
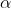

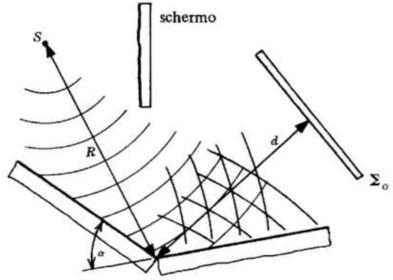

I due specchi riflettono parti diverse dell'onda primaria che proviene da S che quindi
si sovrappongono e interferiscono nella regione davanti a Si può supporre che queste
onde coerenti provengano dalle sue sorgenti virtuali indicate nella figura sottostante.
Si noti che il dispositivo risulta allora identico a quello dell'apparato di Young, per cui
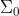
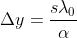
dove ora , la distanza normale tra . In questo caso e
assumendo . Si può quindi scrivere

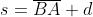



I segmenti possono essere considerati come immagini del raggio incidente
prodotte dagli specchi. Allora, come abbiamo già visto, , e quindi
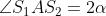
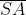

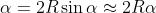
Da qui


7)
Calcolare l'angolo a formato dai due specchi di Fresnel se la sorgente è a 1 m dalla
intersezione dei due specchi, lo schermo è a 2 m da questa intersezione,
e la distanza tra frange consecutive è 1 mm
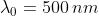
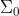
Si sa che Quindi



8)
Ricavare una espressione che dia la distribuzione della intensità di radiazione sul
piano di osservazione relativo a un doppio specchio di Fresnel in funzione di I(0)
(l'intensità di radiazione sull'asse centrale), y (misurata a partire dall'asse), R, d ed
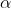
Parlando dell'esperimento di Young (v. problema 1) si è trovato che
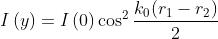
Inoltre e . Quindi



9)
Fresnel ha ideato anche un altro dispositivo a divisione del fronte d'onda detto
biprisma (mostrato nella sottostante figura). Descrivere come funziona e ricavare una
espressione che dia la distanza tra frange consecutive in funzione di R, d,
, n e ,
assumendo che i prismi siano molto sottili .
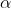
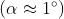


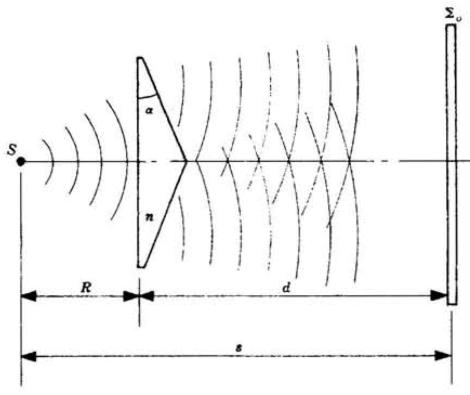
La deviazione minima prodotta da un prisma di indice n nell'aria è data in forma
implicita da
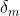
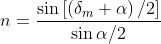
Dato che il biprisma è molto sottile, sia che
sono molto piccoli e
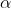
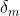

Si può togliere l'indice m dato che i prismi sottili funzionano a deviazione minima o
vicinissimo ad essa, per cui

(Non si confonda questo
con la differenza di fase). Come si può vedere dalla
sottostante figura , il biprisma divide l'onda primaria in due,
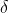

come se sostituisse alla sorgente S due sorgenti virtuali coerenti S1 e S2. L'angolo
e quindi
.
La formula della distanza tra frange consecutive relativa all'apparato di
Young

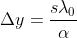

vale anche in questo caso e diventa


10)
Un raggio laser collimato colpisce normalmente un biprisma di
Fresnel. A differenza dall' esperimento di Young, in cui la distanza tra frange
consecutive cresce al crescere della distanza dalla sorgente, in questo caso essa
è indipendente dalla posizione di : dimostrarlo. Determinare nel caso in cui
n = 1,520 e
= 1°30'.
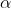
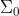



Dal precedente problema:


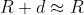
ma ora e quindi . Per cui

Per i valori dati

Si noti che neanche con un valore di
piccolo come 1°30' si ottengono frange
abbastanza distanziate.
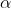

11)
La sottostante figura rappresenta porzioni di un'onda luminosa; una porzione di
essa va direttamente a colpire il piano di osservazione, mentre l'altra vi arriva dopo
essere stata riflessa da una superficie speculare liscia. Questo sistema di divisione del
fronte d'onda è detto specchio di Lloyd. Discutere il meccanismo per cui si producono
frange di interferenza, dedicando particolare attenzione al processo di riflessione.
Ricavare una espressione per l(y).

Il raggio riflesso è come se provenisse da una sorgente virtuale SI' come indicato in
nella sottostante figura. Anche in questo caso si ha una situazione simile per molti
aspetti a quella dell'apparato di Young. La differenza principale è che l'onda riflessa
subisce all'interfaccia una variazione di fase di 180°
Si ricordino le equazioni di Fresnel precedentemente date, che descrivono il processo
di riflessione tramite i coeffìcienti di ampiezza
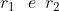

Nel caso di incidenza quasi parallela essi sono entrambi eguali a -1, il che
significa che i vettori campo elettrico incidente e riflesso al contorno sono antiparalleli.
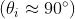
Quindi per qualsiasi punto P

e in alternativa
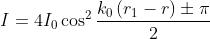

e dato che, come nell'apparato di Young, , si ha

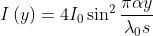
In questo caso in y=0 si ha una frangia scura invece di un massimo

12)
Riferendosi allo specchio di LIoyd del soprastante problema, si supponga che la
sorgente sia situata 2 mm sopra il piano della superficie riflettente e ad 1 m dal
piano di osservazione.
Determinare la posizione del primo massimo se

La distanza tra frange consecutive è data come prima da In questo caso

, per cui

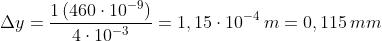
Il centro della frangia scura centrale cade al livello della superficie riflettente. La
frangia scura successiva si trova 0,115 mm sopra questa superficie e il primo
massimo è a mezza strada tra le due a y =0,0575 mm.


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





