



Credimi, i cellulari sono l'unica cosa che gli uomini sono fieri d'avere piccolo!
OTTICA TEORICA

INTERFERENZA E COERENZA

INTRODUZIONE
Nelle precedenti pagine si è trattato della sovrapposizione di stati
ortogonali.
La teoria della interferenza tratta invece soprattutto della sovrapposizione di campi elettrici
complanari.
Come si è visto precedentemente, i fenomeni ondulatori sono descritti da una equazione
differenziale lineare del secondo ordine, per cui vale per essi il principio di sovrapposizione.
Quindi in un punto in cui vengono a sovrapporsi due o più campi ottici, l'intensità del campo
elettrico risultante E è la somma vettoriale delle perturbazioni costituenti.
I campi in alcune regioni si eliminano completamente o parzialmente a vicenda, mentre in
altre regioni i solchi e le creste dell'onda risultante vengono esaltati, grosso modo come per
le increspature in uno specchio d'acqua.
Ne risulta una distribuzione della intensità di radiazione che spesso differisce dalla semplice
somma algebrica delle intensità delle onde componenti.

INTERFERENZA DI DUE ONDE
Si considerino due onde piane polarizzate linearmente e di eguale lunghezza d'onda, date da
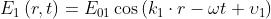

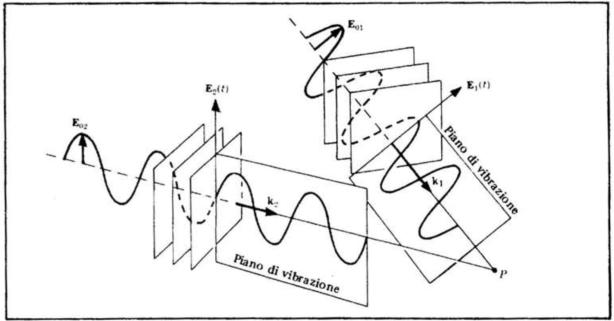
che si sovrappongono nel punto P come nella sottostante figura.
In questo caso sono tutte delle costanti.
Queste onde possono ad esempio provenire da due sorgenti puntiformi molto distanti.
Il campo risultante è semplicemente


Ma dato che nella regione delle frequenze ottiche i campi oscillano a più di
,
la grandezza che riveste un interesse pratico è la intensità di radiazione, che è
direttamente misurabile.
A meno di un coefficiente costante, l'intensità di radiazione può essere espressa come
la media nel tempo del campo risultante


Dove

Ne segue che
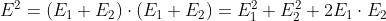
Prendendo la media si ha

Dove , e l'ultimo termine è detto
termine interferenza.
E’ grazie a questo termine che I è diverso dalla semplice somma delle intensità di
radiazione delle onde componenti, cioè da .
La media nel tempo di una data funzione f(t) è data da

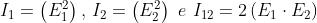
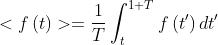
In questo caso il tempo di rilevazione T è molto maggiore del periodo di oscillazione
di un'onda
.
Se si sviluppano i calcoli indicati per le onde piane sopra date , il termine interferenza
diventa


dove la differenza di fase
è data da
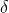
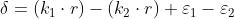
Ciò sta a significare che spostandosi nello spazio da punto a punto, varia r e varia
,
per cui variano sia 112 che
.
Il contributo alla differenza di fase proviene dalla differenza nella
lunghezza del cammino percorso dalle onde nell'andare dai punti sorgente fino a P.
Il contributo è invece dovuto alla differenza di fase iniziale delle emittenti e,
se è costante, come si è supposto, si dice che le emittenti sono coerenti.
Nelle seguenti pagine si esaminerà il caso più generale di coerenza parziale.
Per ora basta una semplice regola: se le onde che si sovrappongono sono coerenti,
i corrispondenti campi elettrici si combinano tra di loro in modo prolungato e per
avere la intensità di radiazione si sommano e quindi si eleva al quadrato. Se invece
le onde non sono coerenti, i singoli campi, che sono effettivamente indipendenti, devono
prima essere elevati a quadrato e poi si sommano le intensità di radiazione delle onde
componenti.
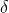
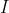
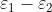

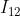

1 )
Si supponga che i campi elettrici delle due onde della soprastante figura siano
paralleli. Ricavare una espressione simbolica di
in funzione di .
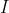

Per la sovrapposizione di onde coerenti
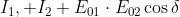
ma ora i campi sono anche paralleli e . Tenendo presente i
risultati di un precedente problema, le intensità di radiazione componenti possono
essere scritte come


Quindi

Per determinare la distribuzione della luce nello spazio basta far passare punto per
punto, determinare il valore di
in ognuno di essi e quindi una volta noti
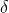
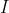
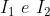

2)
Descrivere la distribuzione della intensità di radiazione che si avrebbe nel caso
esaminato nel precedente problema, se le due onde fossero non coerenti, cioè se
le rispettive fasi variassero a caso e rapidamente rispetto al tempo di rilevazione.
Il termine interferenza

Può essere riscritto nella forma

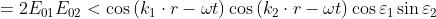

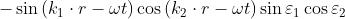

Dato che variano irregolarmente e rapidamente rispetto al tempo di
rilevazione, il valore medio di ognuno dei termini preso rispetto a detto tempo deve
essere nullo, per cui .
In alternativa si noti che la fase relativa varia anch'essa rapidamente
ed a caso e se si pone si ottiene come si prevedeva.
In effetti la figura di interferenza varia così rapidamente che ciò che si osserva
è solo
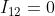
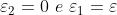
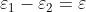
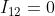
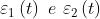

Questo è il motivo per cui quando si ha a che fare con sorgenti non coerenti si può
semplicemente elevare a quadrato i singoli campi e quindi sommare le intensità
di radiazione

3)
Si supponga di far sovrapporre due onde identiche di luce naturale. Ci sarebbe
interferenza? (Cioè sarebbe diverso da zero?)
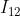
Ognuna delle onde non polarizzate può considerarsi composta da due stati
ortogonali e non coerenti.
Questi a loro volta rispetto ad un qualsiasi piano che interessi (ad esempio il piano
che contiene ) possono essere ìndicati come
Dato che le due onde sono identiche, sono coerenti e tali sono anche
E Di conseguenza ne risultano due figure di interferenza indipendenti, che
si sovrappongono esattamente

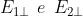
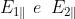


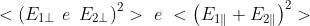
Quindi l'equazione della distribuzione della intensità di radiazione resta valida sia
che le onde siano polarizzate sia che non lo siano, a condizione che esse siano
identiche

4)
Si considerino nuovamente le onde del problema 1) e si studino le condizioni alle
quali I assume valori massimi e minimi.
Dato che
,
si ha quando


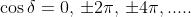
quindi
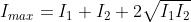
Le due onde sono in fase, i solchi si sovrappongono ai solchi e le creste alle creste,
come nella sottostante figura a).

Analogamente quando , cioè quando e

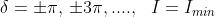

In questo caso isolchi di un'onda si sovrappongono alle creste dell'altra, tendendo
quindi ad eliminarsi a vicenda, come in figura b).
Quando si dice che si ha una interferenza costruttiva, quando invece
1 , si dice he si ha una interferenza distruttiva.



5)
Ricavare una espressione che dia la intensità di radiazione nel punto P della
soprastante figura [1] , supponendo che le ampiezze dei campi siano entrambe
eguali e parallele.
[1]
Dato che i campi sono paralleli, dal problema (1 si sa che

Inoltre che significa che le quali si possono quindi porre
entrambe eguali a ·
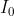


Ciò porta a
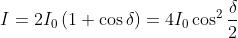
La figura di interferenza varia con il quadrato del coseno.

6)
Michelson definì la visibilità delle frange di una figura di interferenza come
(a) Ricavare una espressione della visibilità per la figura di interferenza delle due
onde coerenti di figura [1] , supponendo che i loro campi siano paralleli.
(b) Qual è la visibilità nel caso in cui le ampiezze dei due campi sono eguali?

(a) Sostituendo direttamente nella formula della visibilità le espressioni di
ottenute nel soprastante problema 4) si ottiene


b) Quando , per cui


In alternativa, dal problema 5), e ancora
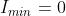
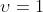

7) Si supponga che il punto P di figura [1] sia spostato più vicino alle sorgenti puntiformi
per cui le onde che lo raggiungono sono sferiche. Si assuma inoltre che le
ampiezze dei campi in P siano eguali e parallele. Discutere la forma assunta dalla
figura di interferenza.

Le onde sferiche nel punto P sono date da


con la geometria illustrata nella soprastante figura. Nel caso in questione

e trascurando un fattore costante, . Quindi, per il problema 5)

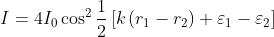
i cui massimi e minimi si hanno rispettivamente per ,
dove m assume i valori Ne segue che i massimi di I corrispondono alle
situazioni in cui
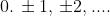
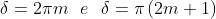
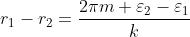
e i minimi a quelle in cui
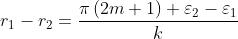
Queste sono entrambe equazioni di famiglie di superfici nello spazio: precisamente
iperboloidi di rotazione concentriche. Nella soprastante figura sono riportate alcune di
queste superfici sulle quali nel caso in cui
.
La regione nella quale sono immerse le due sorgenti è sede di una figura di interferenza
che potrebbe essere messa in evidenza da una serie di frange luminose e frange scure
su di uno schermo.
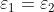


8)
Descrivere la distribuzione di intensità di radiazione che producono a grande
distanza due sorgenti puntiformi di forza eguale , in fase tra loro e la
cui distanza,a, è eguaIe a .

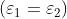

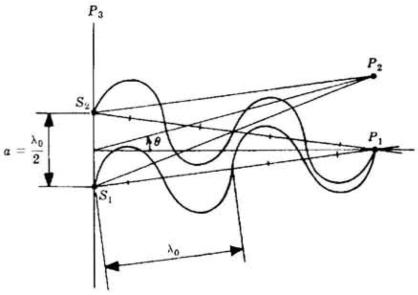
Nella maggior parte dei casi di interferenza
ottica, la distanza tra le sorgenti è
molto grande, ma anche i
casi in cui presentano note-
-vole interesse pratico.
Esaminando la figura a lato si vede
che le distanze sono
eguali (e, nonostante il modo in
cui la cosa è presentata nel disegno,
equivalgono a molte lunghezze d'onda

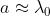

Le onde percorrono cammini ottici di
eguale lunghezza e arrivano in P1 quasi
parallele e in fase, interferendo costruttivamente. Se è l'intensità di radiazione di
ognuna delle sorgenti, la risultante in .
Nel punto , che è anch'esso lontano dalle sorgenti, si assume che i campi
abbiano circa la stessa ampiezza. La differenza di lunghezza dei
cammini ottici è circa
. Ne segue che la differenza tra i numeri di lunghezze
d'onda relativi ai due cammini è .
Dato che ogni onda intera corrisponde a uno sfasamento di
radianti, la differenza
di fase tra le due onde in è


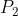

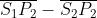
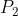

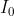
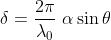
Dal problema 7)

e in questo caso particolare in cui ,
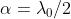
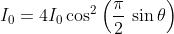
Si noti che in , . In le perturbazioni sarebbero sfasate di
radianti, e si eliminerebbero completamente a vicenda. In questo caso
come già detto.
La sottostante figura dà un grafico polare di I in funzione di e consiste di una figura
a due lobi in accordo col fatto che i massimi di radiazione si hanno per

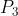
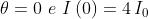
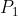
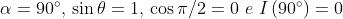




Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





