



Dopo la tua morte sarai ciò che eri prima della tua nascita.
OTTICA TEORICA

DICROISMO E POLAROID

DICROISMO E POLAROID
In senso molto generale dicroismo indica l'assorbimento selettivo di uno dei due stati
ortogonali
che compongono un'onda incidente.
Il termine fu inizialmente usato in riferimento ai cristalli dicroici esistenti in natura come
la tormalina. La luce il cui campo E è parallelo all'asse ottico del cristallo è trasmessa con
poco assorbimento, mentre la componente normale a quest'asse è fortemente assorbita.
Attualmente hanno assunto maggiore interesse pratico i sistemi dicroici artificiali, il
più semplice dei quali è il polarizzatore a reticolo di fili metallici della sottostante figura.
In questo caso un fascio, ad esempio di microonde, non polarizzato cade su una serie di fili
conduttori sottili disposti molto fittamente. Lo stato costituente
parallelo ai fili trascina
gli elettroni interni ai fili, generando quindi in essi una corrente alternata.
In aggiunta al riscaldamento per effetto joule, che corrisponde all'assorbimento di energia
del campo componente verticale, gli elettroni irradiano a loro volta un'onda che tende ad
indebolire ulteriormente questo stato
.
Invece il campo orizzontale subìsce un effetto molto ridotto data la scarsa mobilità degli
elettroni in direzione orizzontale. Ne segue che il fascio luminoso trasmesso è in gran parte
composto di luce polarizzata linearmente in direzione perpendicolare ai fili.
Il moderno polaroid a lamine (H-sheet polaroid) è un qualcosa di simile al reticolo di
fili metallici, ma a livello molecolare. In questo sistema tutte le molecole a catena lunga
di un pezzo di alcool polivinilico trasparente vengono allineate in una data direzione
scaldandolo e stirandolo. La pellicola viene quindi tinta con una soluzione di iodio e
lo iodio si dispone a sua volta lungo le molecole allineate di alcool polivinilico.
Gli elettroni di conduzione associati allo iodio circolano quindi su e giù lungo le molecole
come se queste fossero dei fili microscopici.
Il risultato è un polarizzatore lineare cioè un apparecchio che lascia passare solo luce il
cui campo E sia parallelo ad una direzione data (asse di trasmissione).






1 )
La sottostante figura mostra due polarizzatori lineari tipo polaroid disposti in modo che
i rispettivi assi di trasmissione formino un angolo . Ricavare una espressione della
intensità di radiazione del raggio emergente dal sistema in funzione di .
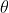
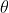
Si supponga che l'ampiezza del campo elettrico che esce dal primo polaroid (il
polarizzatore) sia .
Esso è ruotato di un angolo o rispetto all'asse di trasmissione, verticale, del secondo
polaroid (l'analizzatore) e quindi ha una componente parallela all'asse di trasmissione di
ampiezza .
Da un precedente problema si sa che I varia con il quadrato dell'ampiezza del campo


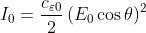
Esso assume il valore massimo per
. Quindi
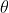

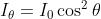
detta legge di Malus

2)
Un raggio di luce non polarizzata con intensità di radiazione è fatto passare
attraverso una successione di due polarizzatori lineari perfetti. Quale deve essere
l'orientamento relativo dei due polarizzatori se si vuole che il raggio emergente
abbia intensità di radiazione (a) , (b) ?



(a) Si supponga che il raggio incidente venga scomposto in due stati
, ortogonali e
non coerenti, ognuno con densità di flusso . Dato che la componente parallela
agli assi di trasmissione non subisce perdite (polarizzatori perfetti), ogni polariz-
-zatore lascia passare .
Quando i due polarizzatori sono allineati con gli assi di trasmissione paralleli, la
intensità di radiazione del raggio emergente è ancora .




(b) Per la legge di Malus è , mentre da (a) . Si vuole
che sia ; in altre parole
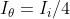

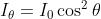

Da cui


3)
Quale deve essere l'orientamento relativo di due polarizzatori lineari perfetti se si
vuole che sotto illuminazione naturale il raggio emergente abbia intensità di radia-
-zione pari alla metà del massimo valore trasmesso?
La intensità di radiazione trasmessa massima si ha per . Si deve quindi avere
un angolo e tale che .
La legge di Malus diventa

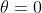

Quindi
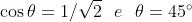

4)
Si considerino due polarizzatori lineari incrociati, uno con l'asse di trasmissione
verticale e l'altro orizzontale. Si inserisca poi tra i due un terzo polarizzatore lineare
con l'asse di trasmissione a 45° rispetto alla verticale. Determinare la intensità di
radiazione emergente prima e dopo l'inserimento del terzo polarizzatore in funzione
di la densità di flusso di un raggio di luce naturale incidente.
E' chiaro che i due polarizzatori lineari con gli assi incrociati a 90° non lasciano
passare luce.
Quando si inserisce il terzo polarizzatore, la luce che esce dal primo polarizzatore è
linearmente polarizzata nella direzione verticale ed ha intensità di radiazione .
Per la legge di Malus, con , la densità di flusso che lascia il polarizzatore
intermedio in direzione del terzo è




L'angolo formato dagli assi di questi due è ancora 45° per cui la intensità di
radiazione finale è

La luce che lascia i tre polarizzatori è uno stato orizzontale.


5)
Tre polarizzatori lineari perfetti sono riuniti normalmente ad un asse centrale
lungo cui viaggia un raggio di luce naturale con intensità di radiazione .
Si supponga che il primo e l'ultimo polarizzatore siano fissi e con i relativi assi
disposti a 90° e che il polarizzatore intermedio ruoti ad una velocità angolare
attorno all'asse: scrivere un'equazione che dà la intensità di radiazione l del raggio
emergente in funzione di
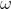

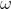
Il raggio che esce dal primo polarizzatore sia polarizzato verticalmente e con una
densità di flusso . Per la legge di Malus la intensità di radiazione che esce
dal secondo polarizzatore (quando esso forma un angolo
con il primo) è
L'angolo formato dal secondo e dal terzo polarizzatore è
. Trascurando ogni effetto dovuto al valore finito di c, la intensità di
radiazione che esce dal terzo polarizzatore è
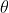

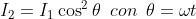
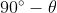

Usando la identità , si ottiene


E' interessante notare che la intensità di radiazione emergente oscilla ad una
velocità quattro volte la velocità di rotazione.

6)
Un raggio di luce polarizzata ellittica dato da
passa normalmente attraverso un polarizzatore lineare ideale ruotato di 45° nel
piano xy.
Ricavare una espressione che rappresenti il raggio emergente e descrivere il suo
stato di polarizzazione.

Per determinare la componente trasmessa di E si definisca un versore parallelo
all'asse di trasmissione del polarizzatore, cioè
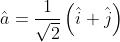
Il prodotto scalare dà il valore scalare della componente cercata:
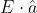

Questi due termini seno possono essere combinati in una unica funzione seno
oscillante nel piano di z e dell'asse di trasmissione; naturalmente il raggio è linearmente
polarizzato. In effetti una coppia qualsiasi di funzioni armoniche aventi la stessa frequenza

si combinano a dare

dove
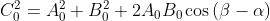

Nel nostro caso e dovremo sostituire a . Quindi




e
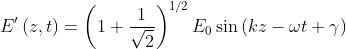
L'intensità di radiazione emergente è quindi

Si può verificare questo risultato facilmente disegnando le due funzioni seno. E'
evidente che la risultante raggiunge un massimo dove le due si incrociano, il che per
simmetria avviene a 67,5°. Questo valore massimo di E' è la sua ampiezza, eguale a
Elevando questa a quadrato si ha , in accordo con quanto ottenuto prima.
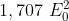
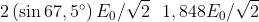

7)
Due polarizzatori lineari ideali con assi di trasmissione orizzontali sono illuminati con
luce naturale. Si supponga di collocare un terzo polarizzatore lineare ideale tra i due
con l'asse di trasmissione a 30° rispetto all'orizzontale; determinare la intensità di
radiazione emergente in funzione della intensità I’ che usciva prima di inserire il
terzo polarizzatore.
Sia l'ampiezza del campo che esce dal primo polarizzatore. Il campo che esce
dal secondo polarizzatore è allora . Il campo che esce dal terzo
polarizzatore è .
La intensità di radiazione corrispondente è allora
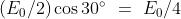
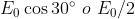


L'intensità di radiazione uscente quando non c'è il polarizzatore intermedio è

Quindi I=I’/16


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





