



Sono un uomo di mondo: ho fatto tre anni di militare a Cuneo
OTTICA TEORICA

POLARIZZAZIONE ELLITTICA

POLARIZZAZIONE ELLITTICA
Luce lineare e luce circolare rappresentano due casi piuttosto speciali. Ambedue comportano
dei valori specifici della fase relativa , e l'ultimo anche la eguaglianza delle ampiezze
componenti.
Un caso molto più generale di sovrapposizione di stati ortogonali dà luce ellittica
o in stato
.
In questo caso la punta del vettore campo descrive, al variare del modulo e della direzione
di E, una ellisse (o, più precisamente, una elica ellittica).
Anche in questo caso si scrivono gli stati componenti, questa volta in forma scalare, come

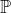

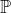
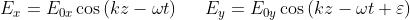

La espressione di può essere sviluppata separando
dalla fase e, dopo alcuni passaggi per far scomparire la
dipendenza esplicita da , si arriva a




Questa è l'equazione di una ellisse ruotata di un angolo
rispetto all'asse come indicato nella figura a lato.
Il valore di
si può ricavare dalla equazione
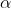
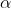

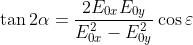

1 )
Verificare che la luce lineare è un caso particolare di luce ellittica.
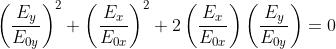
Sappiamo che si ha luce polarizzata linearmente quando e quando
, dove Nel primo caso e

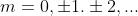

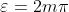
Esprimendo questo quadrato come prodotto di fattori si ha

Questa è l'equazione di una retta (dove le coordinate sono ) passante per il
punto e con pendenza . Analogamente, se
è eguale a zero o
a un multiplo pari di
si ha e




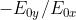


Questa è anch'essa una retta, ma ora con pendenza positiva.

2)
Dimostrare che per luce lineare si ottiene l'equazione
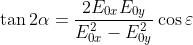
La tangente può essere espressa nella forma

Se l'ellisse di figura [A] degenera nel primo e nel terzo quadrante nel suo asse, si ha
[A]


e quindi
ciò corrisponde naturalmente al caso in cui è zero o un multiplo pari di , Nell'altro
caso ( multiplo dispari di ) la ellisse degenera nel suo asse nel secondo e quarto
quadrante.





3)
Verificare che la luce circolare è un caso particolare di luce ellittica.

Dai precedenti paragrafi si sa che si ha luce circolare quando
In questo caso e



che corrisponde ad un'ellisse i cui assi coincidono con gli assi coordinati .
Quando , si ha , che è l'equazione di un cerchio.


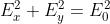

4)
Determinare lo stato di polarizzazione dell'onda i cui stati ortogonali componenti
sono
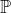


Le ampiezze non sono eguali per cui, anche se la risultante non
è luce circolare.
Dato che e si ha uno stato i cui assi di simmetria sono gli assi
. Esaminando come varia nel tempo l'onda risultante per
si ha
L'onda è polarizzata ellittica sinistra.
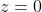



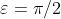


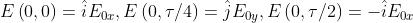
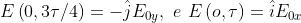
Si noti che essendo il termine dove figura il tempo preceduto dal segno meno, una
positiva fa sì che assuma tutti i valori possibili in anticipo su
per cui si dice che per è in anticipo su .
La sottostante figura generalizza il risultato agli altri valori di dove








è in anticipo su di




5)
Descrivere lo stato di polarizzazione dell'onda
dando anche il suo orientamento
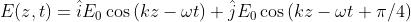
L'onda non è né lineare né circolare, dato che , per cui deve essere ellittica.
Controllandola in si ha

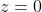

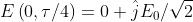

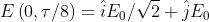
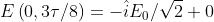




Il campo E ruota in senso antiorario e quindi è polarizzato sinistro. Per determinare
di quanto è ruotata l'ellisse si usa la equazione


6)
Nel precedente problema si ha a che fare con uno stato ruotato di 45°. Quando si
analizza praticamente questa luce, sarebbe di notevole interesse conoscere il massimo
e il minimo valore del campo. Determinare di conseguenza la lunghezza dei semiassi
maggiore e minore dell'onda del problema 5

Il semi asse maggiore si ha per il valore di t intermedio tra 0 e , cioè per .
Ne segue



e

Il semiasse minore si ha un quarto di ciclo dopo, cioè per .

Quindi
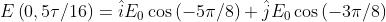
e


7)
La luce ellittica può essere sintetizzata tramite la sovrapposizione di uno stato e
uno stato . Scrivere delle espressioni che rappresentino le onde e che si
propagano lungo l'asse z e che combinate danno uno stato ruotante in senso orario
con il semi asse maggiore parallelo all'asse y
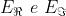




E' evidente che occorrono degli stati che per
z = 0 e t = 0 hanno solo componenti .Per di più, se
la risultante ruoterà in senso
orario assieme allo stato .Quindi
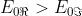
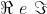
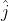



per cui

Il processo è illustrato nella figura a lato


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





