



A che serve guadagnare trofei quando rinunci a essere te stesso?
OTTICA TEORICA

POLARIZZAZIONE PIANA

La luce è un'oscillazione elettromagnetica trasversale e fino a questo punto si sono
considerati solo casi in cui il vettore campo elettrico giace in un piano fisso. Questo
piano è detto piano di vibrazione e la luce è detta luce polarizzata.
Queste pagine si occupano per lo più della sovrapposizione di due onde luminose di eguale
frequenza polarizzate in piani tra loro ortogonali.
Il campo elettrico risultante non giace necessariamente in un piano fisso; il vettore campo
elettrico può anche ruotare nel tempo.
Le ampiezze e le fasi relative delle due onde interagenti determinano lo stato di polariz-
-zazione della perturbazione composta.
Per confronto, si noti che della interazione di onde complanari si occupa la teoria
dell'interferenza delle prossime pagine-
POLARIZZAZIONE PIANA

Si considerino due campi ottici armonici normali tra loro dati da:


Le onde si spostano nel verso positivo delle z ed hanno una fase relativa
. Il piano
di vibrazione di è il piano xz, mentre giace nel piano yz.
La perturbazione risultante


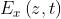
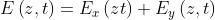
varia con
. Nel caso particolare in cui
=0 o un multiplo intero di
i campi
componenti sono in fase e


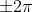
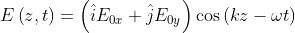

L'ampiezza, è costante e anche l'onda risultante è polarizzata in un
piano o polarizzata linearmente, come indicato nella soprastante figura (a).
Analogamente, quando è un multiplo intero dispari di i campi componenti sono
sfasàti e

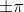
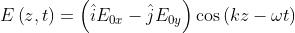
Anche in questo caso la risultante ha ampiezza costante e l'onda è polarizzata
linearmente, come indicato nella soprastante figura (b).
Per indicare una perturbazione ottica polarizzata linearmente si usa spesso anche
l'espressione luce in stato
.


1 )
Entrambe le onde
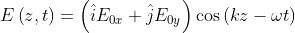
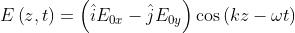
rappresentano luce in stato . Dimostrare che in generale onde del genere non
sono ortogonali. A quali condizioni i piani di vibrazione saranno tra di loro normali?


Detti i vettori ampiezza rispettivamente di il loro prodotto scalare è
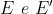


dove
è l'angolo formato da . Ma
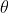

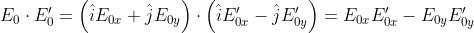
Quindi

e
generalmente è diverso da 90° dato che il secondo membro di questa equazione
generalmente non è nullo. Se però ,ilsecondo membro si annulla e
le onde sono ortogonali. Probabilmente il caso più semplice in cui ciò avviene si ha
quando .
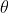
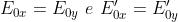


2)
Scrivere una espressione che rappresenti un'onda polarizzata linearmente di
frequenza angolare
che si propaga nella direzione delle z positive con un
piano di vibrazione che forma un angolo di 30° con il piano zx.

Sia il valore scalare dell'ampiezza dell'onda. Allora le componenti secondo l'asse
x e y sono
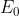
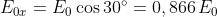

Quindi
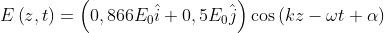
dove la costante ignota
dipende dalle condizioni iniziali
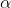

3)
Scrivere una espressione che rappresenti una perturbazione polarizzata linearmente
di frequenza angolare
che si propaga nella direzione delle z positive e tale che
per t = 0 e z = 0 il campo E formi un angolo di 120° con la direzione positiva delle x.
Verificare che questa onda è ortogonale all'onda del problema 2)

Detta la ampiezza scalare,
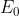
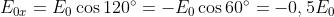

Quindi

Per verificare che quest'onda è ortogonale a quella del menzionato problema, si
esegua il prodotto scalare delle ampiezze, cioè

Dato che questo è nullo, i piani di vibrazione sono normali.

4)
Descrivere l'onda rappresentata dalla funzione



dove e sono i versori base delle coordinate cartesiane.
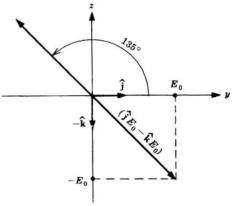
L'onda può essere scritta anche nella forma
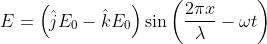
Essa si propaga nella direzione positiva delle x con
un'ampiezza costante di e quindi è polariz-
-zata linearmente. Il piano di polarizzazione è ruotato
di 135° rispetto al piano xy, come indicato in
figura a lato. Si noti che l'ampiezza scalare di E è .
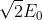


5)
Descrivere l'onda che risulta dalla sovrapposizione delle perturbazioni

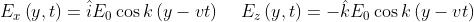
Disegnare per
(dove
ovviamente
è il periodo).
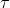
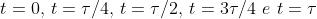
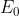
Dato che
, si può scrivere come


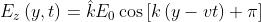
dove la fase relativa è proprio . La risultante è quindi polarizzata linearmente.
La fase di , può essere scritta come , mentre quella di come
.
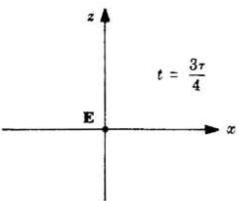
Quindi per y = 0,

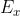

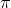






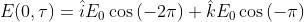
Qui sotto sono riportate le perturbazioni corrispondenti






Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





