



Non può esserci vera libertà senza la libertà di fallire
OTTICA TEORICA

PROBLEMI SUPPLEMENTARI

SUPERFICI RIFRANGENTI NON SFERICHE
1)
Si consideri nuovamente l'ovoide di Cartesio già visto e si costruisca un sistema di
assi coordinati con l'origine nel vertice V; con l'asse x lungo la retta SP e l'asse y
perpendicolare ad esso. Ricavare ora una equazione dell'ovoide in termini di
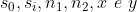
Risp.
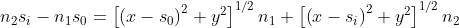
2)
Si supponga di avere un sistema di assi coordinati x-y rispettivamente orizzontale e
verticale, con l'origine nel vertice della interfaccia curva che divide due mezzi .
Dimostrare che se si vuole che le onde piane che arrivano da sinistra siano focalizzate
in P il profìlo dell'interfaccia deve essere

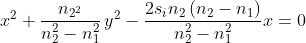
Dimostrare che per la interfaccia è un ellissoide di rotazione. Determinare le
lunghezze dei semiassi maggiore e minore, a e b, e la eccentricità e

Risp.


3)
Il fascio di raggi paralleli assiali che nella sottostante figura arrivano da sinistra sembra
provenire dal punto P, essendo . Ricordando che in questo caso è una
grandezza negativa, dimostrare che il profilo dell'interfaccia ha la stessa equazione
considerata nel precedente problema .
Dimostrare che si tratta di un iperboloide di rotazione. Suggerimento: sfruttare il fatto
che , dove C è situato sull'arco descritto dal punto B nella rotazione
di . Il punto P è il primo fuoco dell'iperboloide a due falde.






SUPERFICI RIFRANGENTI SFERICHE
4)
Una bacchetta di diamante (nd = 2,42) con una estremità infilata in una semisfera
convessa presenta un piccolo difetto nero. Supposto che il raggio di curvatura sia di
20 cm e che il difetto si trovi sull'asse centrale a 20 cm dal vertice, dove apparirà la
sua immagine quando la bacchetta è immersa in acqua (nw = 1,33)?
Risp. Oggetto in C; quindi = -20 cm, quale che sia il mezzo circostante.


5)
Una lunga bacchetta di vetro (ng = 1,5) di 10 cm di diametro è immersa in aria.
L'estremità sinistra ha la forma di una semisfera convessa e quella destra di
iperboloide concavo.
L'iperboloide ha eccentricità 1,5 e il vertice 5 cm a destra del primo fuoco F1
Dove deve essere posta una sorgente assiale puntiforme perché la bacchetta dia di
essa una immagine virtuale in F1?
Risp. Per la superficie sferica = 10 cm e quindi = 10 cm a sinistra



6)
Una sfera di crown borosilicato (no = 1,5) di raggio 4 cm è circondata da alcool
etilico (ne = 1,36). Una formica che va alla deriva nell'alcool si trova a 6 cm dal
centro della sfera; descrivere la sua immagine.
Risp. = -2,32 cm (immagine virtuale a sinistra del vertice).


EQUAZIONE DELLA LENTE SOTTILE

7)
I raggi di curvatura di una lente sottile di vetro (n = 1,5) biconvessa sono nel
rapporto 2 a 1. Ricavare una equazione per R, il raggio più piccolo, in funzione della
distanza focale.
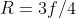
Risp.

8)
Una lente sottile positiva di distanza focale f è posta tra una sorgente puntiforrne S e
uno schermo, distanti l'uno dall'altro L. Ricavare una espressione per le due
posizioni della lente (misurate da S) per le quali si hanno sullo schermo immagini
reali.
Risp.


9)
Una lente sottile di flint (nl = 1,65) equiconvessa ha distanza focale di 62 cm
quando è immersa in aria.
Determinare il raggio di curvatura.
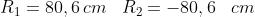
Risp.


10)
Nella figura a lato è indicato un fascio di raggi
convergenti che colpiscono una lente sottile
divergente.
Descrivere quello che capita e usare quindi la
equazione della lente sottile per verificare le
conclusioni. Si noti che .
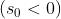
Risp. Il punto A definisce la punta di un oggetto virtuale, mentre B è il corrispondente
punto immagine. Dato che , la immagine è reale, diritta e ingrandita e



IMMAGINI FORMATE DA UNA LENTE SOTTILE SEMPLICE
11)
Si usa una lente sottile positiva per proiettare l'immagine ingrandita di un vetrino su
una parete distante 10m. Se il vetrino è 20 x 30 mm e se si vuole che l'immagine
sia 2 x 3 m, quale deve essere la distanza focale della lente e la distanza tra questa
e il vetrino?
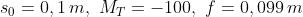
Risp.

12)
Una lente sottile positiva dà di un oggetto alto 5 cm posto a 90 cm dalla lente una
immagine diritta alta 8 cm. Calcolare la distanza focale della lente e la posizione
dell'immagine.
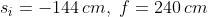
Risp.

13)
Una macchina fotografica semplice consiste di una lente sottile positiva che genera
una immagine reale sul piano della pellicola. Si supponga che la lente abbia distanza
focale 50 mm.Che distanza ci deve essere tra la macchina fotografica e un oggetto
alto 1 m se si vuole che l'immagine sia alta 25 mm? Che distanza ci deve essere tra
la lente e il piano della pellicola ?
Risp.
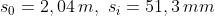

14)
Si consideri una lente sottile tale che tra l'oggetto e la sua immagine vi sia una
distanza L. Dimostrare che


LENTI SOTTILI COMPOSTE
15)
Le lenti di una macchina fotografica con teleobiettivo per lo più somigliano al
telescopio galileiano, consistono cioè di una lente positiva L1 seguita da una lente
negativa L2. Se la lente L1 ha una distanza focale di 20 cm e la lente L2 di -40 cm
e le due lenti sono distanti 10 cm, determinare la f.f.l. e la b.f.l.
Risp. f.f.l. = 33,33 cm, cioè il punto focale oggetto è a sinistra di L1;
b.f.l. = 13,33 cm, cioè il punto focale immagine è a destra di L2

16)
Tre lenti sottili di distanze focali rispettivamente f1= 10 cm, f2 = 20 cm e
f3 = -40 cm e sono a contatto, formando un tutto unico. Descrivere l'immagine
formata da un oggetto posto 16 cm prima delle lenti.
Risp.


17)
Due lenti sottili positive sono a contatto e formano una lente composta di distanza
focale 30 cm. Quali sono le loro due distanze focali se la potenza di una delle lenti
componenti è doppia di quella dell'altra ?
Risp. 45 cm, 90 cm

18)
Su una tavola sono disposti un oggetto, a 12 cm da esso una lente sottile positiva di
distanza focale 9 cm e a 21 cm da questa una lente sottile negativa di distanza
focale -18 cm. Determinare la posizione dell'immagine formata dal sistema.

Risp.
(l'immagine è 90 cm a destra della lente negativa).

LENTI SPESSE
19)
Si consideri una lente spessa con indice di rifrazione 2, i cui raggi di curvatura siano
eguali e negativi.
Descrivere le caratteristiche della lente supponendo che i centri di curvatura siano
distanti d e che la lente sia immersa in aria.
Risp.
La lente è positiva dato che , per cui i
piani principali sono esterni e a destra, distanti d.
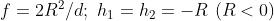

20)
Una lente spessa di vetro (ng = 1,5) biconvessa ha raggi di 2 e 4 cm e spessore 2
cm. Determinare la posizione dei punti principali e dei fuochi rispetto ai vertici
V1 e V2.
Risp.
f= 12 cm, h1 = +0,5 cm, h2 = -1,0 cm

21)
Una lente convergente semisferica di raggio +12 cm ed indice di rifrazione 2,0 è
posta a 36 cm da un oggetto puntifonne posto sul suo asse. Determinare la posizione
dei piani principali e focali e descrivere l'immagine.
Risp. f= 12 cm; h1=0 (primo piano principale in V1) -6 cm (cioè a sinistra di
V2); si=18 cm, a destra di h2, l'immagine è reale.
; h2=

22)
Una lente spessa con indice di rifrazione 2 è tale che entrambe le facce hanno un
centro di curvatura comune e situato all'esterno della lente. Descrivere le carat-
-teristiche della lente, indicando con d il suo spessore.
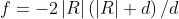


Risp. (lente negativa); .
Si noti che coincidono con il centro di curvatura.

23) Qual è la distanza focale nell'aria di una gocciolina sferica di benzene (nb = 1,501)
di raggio 2 mm? Descrivere l'immagine che essa forma di un oggetto alto 0,5 mm e
posto a 5,3 cm dal centro della gocciolina.
Risp. f=3 mm;
= 3,18 mm dal centro della sfera, = -0,06,
= - 0,03 mm
(l'immagine è reale, rimpicciolita e capovolta).

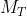

COMBINAZIONI DI LENTI
24)
L'oculare di Huygens è una combinazione di due lenti sottili piano-convesse. La
prima è nota come "lente di campo" e la seconda, più vicina all'occhio dell'osservatore,
come "lente dell'occhio". Si supponga che la lente di campo abbia distanza focale di
3 e la lente dell'occhio . Ambedue hanno la faccia curva a sinistra e sono distanti
tra loro 2 . Un fascio di raggi convergenti sul primo piano focale dell'oculare
emerge come fascio di raggi paralleli. Determinare la posizione del primo piano
focale.
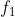
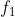
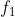
Risp. . Il primo piano focale è situato tra le due lenti,
a sinistra della lente dell'occhio.
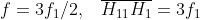
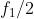

25)
Due lenti sottili positive di distanze focali rispettivamente 40 e 60 cm sono disposte
a 20 cm di distanza.
Dove si deve mettere un oggetto se si vuole che la sua immagine si disponga su
uno schermo 45 cm a destra della seconda lente?
Risp. f= 30 cm, , ; oggetto 50 cm a sinistra della
prima lente o 60 cm da
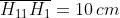

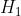

26)
Supponete di avere tre lenti sottili, due convergenti e una divergente, di distanze
focali rispettivamente .
Le prime due lenti sono distanti 6 cm tra di loro e le ultime due 1,4 cm.
Quale deve essere la distanza focale della terza lente se si vuole che il sistema
sia afocale, cioè che i raggi che entrano paralleli escano ancora paralleli.

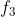
Risp. Combinando le prime due lenti si ha
La terza lente è a distanza d = 6,2 cm da questa combinazione e affinché la
potenza risultante sia nulla deve essere .
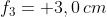
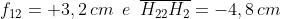

27)
Un «oculare di Ramsden» consiste di due lenti sottili piano-convesse, ognuna di
distanza focale , distanti con le facce curve contrapposte. Determinare in
quale posizione, davanti all'oculare, deve essere il piano dell'oggetto perché i
fasci divergenti di luce provenienti da un qualsiasi punto di , escano come
fasci di luce collimata. In pratica, una lente obiettivo formerà una immagine reale
su (dove ci potrebbero essere anche un paio di capelli incrociati), che è convertita
dall'oculare in raggi paralleli per cui l'occhio la può osservare restando in posizione
rilassata (non contratta).




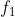
Risp. deve trovarsi a una distanza eguale alla distanza focale effettiva



28)
Una lente sottile convergente con una potenza di 3,33 diottrie è a 1/4 m da una lente
sottile divergente di -20 diottrie. Determinare la distanza focale della combinazione.
Risp. Il sistema è afocale; quando dei raggi paralleli cadono su di esso, emergono
ancora paralleli

SPECCHI PIANI, NON SFERICI E SFERICI
29)
Un oggetto posto a 300 cm da uno specchio sferico concavo genera una immagine
reale a 150 cm dal vertice dello specchio. Dove si deve spostare l'oggetto se si vuole
che la nuova immagine si trovi nella posizione originariamente occupata dall'oggetto?
Risp.
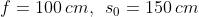

30)
Si supponga che la lente composta del problema 18) sia disposta in maniera tale
che la sua lente negativa posteriore sia a 60 cm dal vertice di uno specchio sferico
convesso di 15 cm di raggio. Determinare la posizione dell'immagine che lo
specchio forma di un oggetto posto a 12 cm dalla prima lente.
Risp. ; l'immagine è virtuale, capovolta e a 10 cm a destra del vertice
dello specchio.


31)
Un cono di raggi converge in un punto S dell'asse a distanza d dietro uno specchio
convesso di distanza focale . In altre parole S è un oggetto virtuale e
. Usare la equazione dello specchio per descrivere la immagine che
ne risulta. (Ricordarsi che )



Risp. L'immagine è reale, diritta, ingrandita e più lontana dallo specchio di quanto
lo sia l'oggetto .


32)
Un oggetto alto 1 cm è situato davanti ad uno specchio sferico concavo con raggio
di curvatura 8 cm ad una distanza di 12 cm. Dare una descrizione completa dell'im-
-magine che ne risulta.
Risp. (immagine capovolta, reale, alta 1/2 cm)
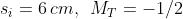

33) Un oggetto alto 4 cm è situato davanti ad uno specchio convesso di distanza focale
-400 cm ad una distanza da esso di 200 cm. Descrivere l'immagine che ne risulta
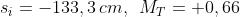
Risp.
(immagine virtuale, diritta e rimpicciolita)

34)
Un oggetto alto 3 cm è posto a 180 cm da uno specchio sferico convesso con raggio
di curvatura di 90 cm. Descrivere l'immagine che ne risulta.
Risp.

(immagine virtuale, diritta, alta 3/5 cm


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





