



Un uomo è libero nel momento in cui desidera esserlo
OTTICA TEORICA
LENTI SPESSE E COMBINAZIONI DI LENTI



LENTI SPESSE
Si consideri di aver collocato una sorgente puntiforme S sull'asse di una lente spessa
a distanza tale che i raggi escano dalla lente paralleli, come nella sottostante figura (a).
E' evidente che la distanza tra S ed il vertice Vi corrisponde a ciò che abbiamo già chiamato
distanza focale frontale (f.f.l.).
Analogamente, un fascio di raggi paralleli che colpisce la lente verrà concentrato in un punto
a destra di V2 a una distanza eguale alla distanza focale posteriore (b.f.l.), come nella
sottostante in figura (b).


Se si prolungano i raggi in arrivo e in uscita (come fatto in figura con linee
tratteggiate), i prolungamenti si incontrano su delle superfici. Nell'ambito dell'approssima-
-zione parassiale queste superfici si riducono a piani detti primo e secondo piano principale;
i punti di intersezione di questi con l'asse ottico, , sono detti rispettivamente primo
e secondo punto principale.
Per lenti di vetro in aria, è approssimativamente eguale a un terzo dello spessore
(d = ) della lente. Si noti che i piani principali non si trovano necessariamente
all'interno della lente.
II caso più semplice e più comune è quello di una lente di indice nt immersa in aria, .
La formula gaussiana della lente

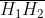
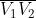

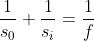
è applicabile anche alle lenti spesse a condizione di misurare le distanze dell'oggetto
e della immagine rispettivamente da e da . La distanza focale, riferita ora anch'essa
ai piani principali, è da


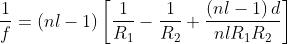
che ovviamente si riduce all'equazione data per le lenti sottili quando lo spessore
della lente diventa trascurabile . La posizione dei piani principali rispetto ai
vertici è a loro volta data da


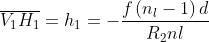

Sia che sono positivi quando i piani principali si trovano a destra dei corrispondenti
vertici V1 e V2.
Le relazioni esistenti tra le varie distanze sono indicate nella sottostante figura. Si noti
che un raggio che parte da un qualsiasi punto del primo piano principale lascia la lente
come se partisse da un punto del secondo piano principale posto alla stessa distanza sopra
o sotto l'asse.
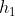




1 )
Dimostrare che anche nel caso di lenti spesse vale la equazione newtoniana della
lente.
Usando le distanze definite nella soprastante figura, si ha e .
Si può quindi riscrivere la equazione gaussiana nella forma



ottenendo
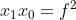

2)
Ricavare una equazione per l'ingrandimento trasversale di una lente spessa.
Per definizione l'ingrandimento è
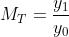
Nella solita soprastante figura, i triangoli e sono simili e così pure i
triangoli . Quindi

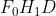
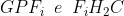

Si tenga presente che misurata sotto l'asse è una grandezza negativa. Dato che
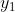


Da ognuna di queste relazioni si ricava una equazione per il rapporto Ne segue
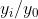

che è eguale alla formula trovata per le lenti sottili.

3)
Quali tipi di lenti di vetro immerse in aria presentano una distanza focale
indipendente dallo spessore?

Dato che
la dipendenza da d si annulla nel caso che .
Quindi sia le lenti piano-convesse che le lenti piano- concave rispondono alla condizione
posta.


4)
Dimostrare che sia per lenti spesse piano-concave, sia per lenti spesse piano-
convesse, uno dei piani principali è sempre tangente alla superficie curva.
Si consideri un fascio di raggi paralleli che colpiscono normalmente la superficie
piana della lente. Tutta la deviazione subita dai raggi si ha sulla seconda superficie,
sia essa concava o convessa. I punti di ìntersezione dei raggi giacciono quindi tutti
sulla seconda superficie della lente. Solo nell'ambito della approssimazione parassiale
questa superficie curva si riduce al piano principale, che quindi è tangente alla
superficie della lente nel vertice. Si può anche ragionare cosi: nel caso in esame
e quindi


indipendentemente dal valore di


5)
Nella sottostante figura (a) sono indicati i piani principali e focali di una lente spessa.
Determinare graficamente il punto immagine coniugato corrispondente al punto
oggetto S .

[A]

[B]
Anzitutto si traccia un raggio arbitrario da S al primo piano principale ( in figura [B]).
Il raggio deve passare per il punto B ma con quale inclinazione?
Per rispondere a questa domanda si traccia un raggio passante per e parallelo a .
Esso arriva in C, passa per D e interseca il piano focale posteriore in E.
Dato che e sono paralleli, essi devono convergere nello stesso punto del
piano focale, cioè in E.
Prolungando la retta si ottiene il punto immagine P.

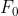





6)
(a) Ricavare una equazione per la distanza focale della palla di vetro di una
indovina in funzione del relativo raggio R e indice di rifrazione n.
(b) Determinare la posizione dei suoi punti principali.
(c) Dove viene focalizzata la luce solare da una palla di 8 cm di diametro e indice di
rifrazione 1,5?
(a) Dato che , sostituendo nella equazione della distanza
focale si ha


(b) I punti principali si trovano in
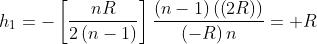
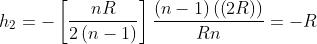
Cioè è a distanza R a destra di mentre è a distanza R a sinistra di .
Ovviamente i piani principali coincidono e passano per il centro della palla.

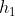

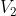
(c) Per una sfera di 8 cm, da (a) si ha
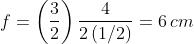
e il punto focale è a 2 cm dal vertice.

7)
Per riprodurre su uno schermo una immagine reale di una finestra si usa una sfera
di vetro (ng = 1,5) di 10 cm di diametro. Dove si deve mettere lo schermo se la
finestra è a 3 m dal centro della sfera?
Che ingrandimento si avrà?
Dal precedente problema

La equazione gaussiana diventa allora
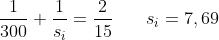
misurata a partire dal secondo piano principale (cioè dal centro della sfera).
In un precedente problema si è visto che l'ingrandimento è eguale a quello
delle lenti sottili:
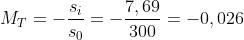
L'immagine è reale, rimpicciolita e capovolta

8)
Una lente biconvessa ha raggi di 5 cm e 20 cm, spessore 2 cm e indice 3/2.
(a) Determinare la posizione dei punti principali e focali e determinare la distanza
dell'immagine per un oggetto posto 16,4 cm a sinistra di V1.
(b) Determinare i valori della f.f.l. e della b.f.l.
(a) Sostituendo nella equazione della distanza focale si ottiene

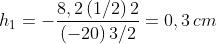
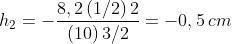
L'equazione gaussiana della lente dà

(b) Per i valori trovati in (a):


COMBINAZIONI DI LENTI
Si possono combinare due o più lenti spesse formando una lente composta, di cui è
dato un esempio nella sottostante figura. La distanza focale effettiva del sistema è data da


in funzione delle distanze focali ( ) delle lenti componenti e della loro distanza
d.
Ogni lente componente ha la sua coppia di punti principali ( ), e così
pure la lente
composta ( ). Quindi un raggio di luce collimata che colpisce la lente composta
viene concentrato in un fuoco a distanza . Le espressioni
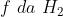
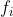
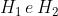

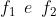

danno le posizioni di .
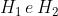
Per un sistema di lenti sottili i piani principali delle singole lenti si sovrappongono ed
diventa semplicemente la distanza tra i centri delle due lenti, come nella sottostante
figura
Un tale sistema si comporta come una lente spessa la cui distanza focale e i cui
punti principali sono dati dalle espressioni appena viste.
In effetti il procedimento seguito combina due lenti (spesse o sottili) in una sola.
Quindi quando si ha a che fare con un sistema centrato di cinque o sei lenti, si possono
affrontare i problemi relativi sostituendo ordinatamente le lenti due a due fino ad
ottenere una unica lente che sta a rappresentare l'intero sistema.
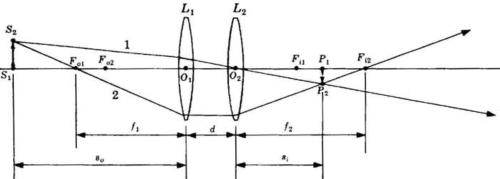

1 )
Due lenti spesse biconvesse eguali sono allineate a 25,7 mm di distanza come in
figura [A].
Ogni lente ha raggi di 60 e 40 mm, spessore 20 mm e indice 1,5. Calcolare la
distanza focale di ogni lente e determinare la posizione dei punti
Determinare la distanza focale effettiva del sistema immerso in aria.
[A]

La distanza focale delle singole lenti è data da
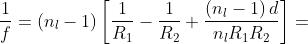
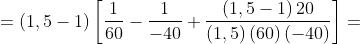

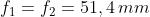
e infine . I punti principali delle singole lenti si trovano


Dato che le lenti sono eguali, questi valori determinano la posizione dei piani
principali rispetto ai vertici di entrambe le lenti.
La lente composta ha una distanza focale data da



2)
Si supponga che le lenti rappresentate nel soprastante disegno [A] siano disposte
in modo che si fronteggino i lati a curvatura minore.
Tracciare uno schizzo del sistema e determinare la posizione dei suoi piani principali
( ). Tracciare un raggio che entri nel sistema parallelamente all'asse.
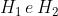
Basta calcolare
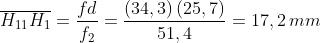
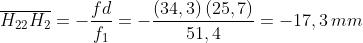
Si ricordi che i valori positivi di queste grandezze sono misurati a destra, come nella
sottostante figura. Attraverso le lenti sono tracciati due raggi: quello superiore è
tracciato facendo lo deviare ai piani principali delle lenti componenti, mentre quello
inferiore è tracciato usando solo H1 e H2.
l due procedimenti si equivalgono


3)
Si consideri una lente composta fatta da una lente sottile positiva seguita a 20 cm di
distanza da una lente sottile negativa. Se le due lenti hanno distanze focali rispet-
-tivamente +40 cm e -40 cm, determinare il valore della f.f.l. e della b.f.l.
Si applica l'equazione


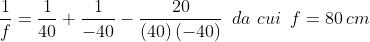



Il problema è illustrato nella soprastante figura. Ovviamente, dato che la f.f.t. e la b.fJ.
sono misurate dai centri delle lenti sottili ai punti focali (Fo e Fi ), i relativi valori sono
rispettivamente 120 e 40 cm

4)
In un tubo di cartone lungo 120 mm sono montate una lente piano-convessa di
raggio 60 mm e indice 1,5 e davanti ad essa una lente biconcava di distanza focale
-60 mm.
Determinare la distanza focale effettiva del sistema e l'immagine da esso data di una
formica lunga 3 mm che si trova 180 mm davanti ad esso.
La lente positiva ha distanza focale
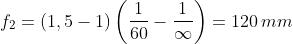
Quindi la distanza focale effettiva del sistema è
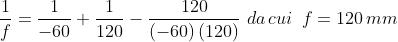
Inoltre


Misurata da , la distanza dell'oggetto è e quindi


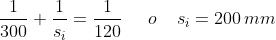

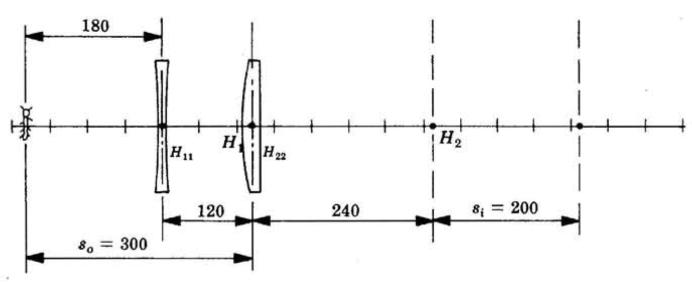
L'immagine si trova 200 mm alla destra di come nella sottostante figura.
L'ingrandimento è quindi

e la formica risulta capovolta e rimpicciolita.


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





