



Vicino alla sua tana, la volpe non fa mai danno
OTTICA TEORICA

IMMAGINI OTTENUTE CON UNA LENTE SOTTILE

IMMAGINI OTTENUTE CON UNA LENTE SOTTILE SEMPLICE.
Abbiamo visto che un fascio di raggi paralleli all'asse viene da una lente positiva
focalizzato in un solo punto.
In realtà ogni fascio di raggi paralleli viene fatto convergere in un fuoco situato su una
superficie passante per , come indicato nella sottostante figura.
Nell'ambito della approssimazione parassiale, è piana ed è detta secondo piano focale,
o piano focale posteriore.
Analogamente si considera un primo piano focale o piano focale anteriore, perpendicolare
all'asse ottico in .



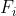
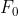
Esamineremo ora - dapprima graficamente e poi analiticamente -- l'immagine di un
oggetto finito formata da una lente sottile.
Per ogni punto dell'oggetto vi sono tre
raggi di cui è particolarmente semplice
seguire il percorso attraverso la lente (vedi
figura a destra). Un raggio (n. 1) che passa per O, il
centro della lente, non viene deviato e
quindi resta una linea retta. Un raggio
(n. 2) che arriva alla lente parallelo all'asse
ottico e passa per . Analogamente un
raggio (n. 3) che passa per ed esce dalla
lente parallelo all'asse ottico. Ne segue che
basta tracciare due soli di questi tre raggi
per ogni punto dell'oggetto: il loro punto di
intersezione è il punto immagine.
Nell'affrontare analitica mente il problema torna utile un'altra formulazione dell'equazione
della lente. Questa formulazione detta newtoniana è
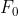

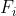
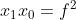
Le grandezze che vi figurano sono chiarite nella sottostante figura e la convenzione dei
segni associata è quella di tabella della precedente pagina.

Si osservi che ,trattandosi qui di lenti sottili, la distanza può essere misurata rispetto
ad un piano centrale passante per O. Inoltre si possono disegnare i raggi come se essi
subissero una sola rifrazione sul piano centrale, invece che su entrambe le interfacce.
La grandezza ( ) dell'immagine ha ovviamente una notevole importanza;
l'ingrandimento lineare trasversale ( ) è definito come
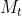


Dai triangoli simili si ha

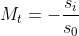

Quando l'immagine è diritta, è positivo e è positivo.
In tabella [A] sono riassunti i significati fisici dei segni delle diverse grandezze, mentre
in tabella [B] sono elencate le proprietà dell'immagine per lenti convesse e lenti concave
sottili.
Si tenga presente che una immagine reale può essere raccolta direttamente su uno
schermo, mentre per una immagine virtuale (come quella che si ottiene con uno
specchio piano) ciò non è possibile.
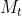

Tabella [A] Il significato fisico dei segni dei parametri
di lenti sottili e interfacce sferiche


Grandezza
Segno +
Segno -
Oggetto reale
Oggetto virtuale
Immagine reale
Immagine virtuale
Lente convergente
Lente divergente
Oggetto dritto
Oggetto capovolto
Immagine dritta
Immagine capovolta
Immagine dritta
Immagine capovolta
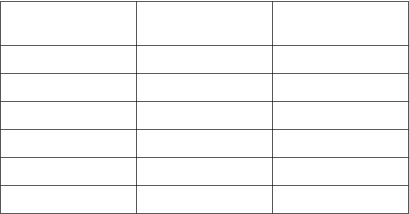


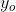
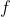


Tabella [B] Caratteristiche delle immagini di oggetti reali ottenute con lenti sottili [CONVESSE]


Posizione
Oggetto
Tipo Immagine
Posizione
Immagine
Orientamento
Immagine
Grandezza
Immagine
reale
capovolta
rimpiccolita
reale
capovolta
di uguale grandezza
reale
Three
capovolta
ingrandita
virtuale
dritta
ingrandita

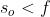


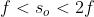

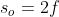
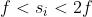
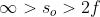
Tabella [C] Caratteristiche delle immagini di oggetti reali ottenute con lenti sottili [CONCAVE]


Posizione
Oggetto
Tipo Immagine
Posizione
Immagine
Orientamento
Immagine
Grandezza
Immagine
qualsiasi
virtuale
dritta
rimpiccolita



1 ) Data una lente sottile biconvessa, calcolare le distanze a cui devono essere l'oggetto e
l'immagine se si vuole proiettare direttamente su uno schermo l'immagine a grandezza
naturale. La lente ha i due raggi eguali e di 60 cm e nlm = 1,5.
La distanza focale è semplicemente
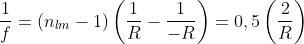
o 1 = R = 60 cm (questo risultato è da tenere a mente; dà una buona idea della
relazione che c'è tra f e R anche se quello considerato è un caso particolare). Dalla
soprastante tabella risulta che una immagine reale e a grandezza naturale si ha per
~r .Si noti che , cioè l'immagine è capovolta.

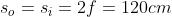

2)
Un tappo di bottiglia alto 3 cm è posto a 75 cm da una lente sottile positiva di 25 cm
di distanza focale. Dare una descrizione completa della sua immagine, usando la
formulazione gaussiana. Verificare la risposta con tabella [B].
Dato che so = 75 cm e f = 25 cm, dalla equazione della lente sottile si ha

Cioè un valore positivo, il che significa che l'immagine è reale e posta a destra
della lente. Per determinare le dimensioni dell'immagine si può usare la formula

Si ha quindi

L'ingrandimento è -1/2 e quindi yi= -1,5 cm. L'immagine è rimpicciolita e capovolta
(MT < 0).

3)
Risolvere nuovamente il problema 2), usando ora solo la formulazione newtoniana.
Dato che
ne segue
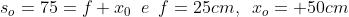

Ma naturalmente
come nel precedente problema.
Quanto alle dimensioni dell’immagine,


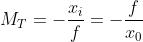
ed entrambe le formule vanno bene. Quindi

4)
Si vuole produrre con una lente sottile piano-convessa una immagine reale grande il
doppio dell'oggetto. Supposto che la lente abbia un raggio di curvatura di 50 cm e un
indice di rifrazione di nlm = 1,5, determinare la posizione dell'oggetto e dell'immagine
rispetto alla lente (a) usando l'espressione newtoniana, (b) usando l'espressione
gaussiana.
(a)
Dalla soprastante tabella [B] risulta che una immagine reale e ingrandita si ha
per e che questa sarà capovolta e collocata in modo che .
In questo caso
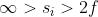

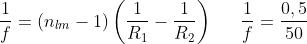
cioè f = 100 cm. Quindi, dato che


Con
, e quindi


(b) La formula gaussiana

unita al fatto che
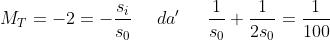
e come in (a)
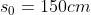

5)
Si supponga che un oggetto posto 20 cm a sinistra di una lente positiva abbia
l'immagine 60 cm a destra della lente. Dove andrà a collocarsi l'immagine se si sposta
l'oggetto a 5 cm dalla lente? Dare una descrizione completa dell'immagine nei due casi
La distanza focale della lente si può ricavare dalla equazione della lente sottile :
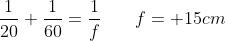
Inoltre

e quindi l'immagine è reale, capovolta e ingrandita (come si poteva ricavare dalla
tabella [B] per ).


Nel secondo caso
Ora l'immagine è virtuale, diritta (MT = +1,5), ingrandita e posta a 7,5 cm a sinistra
della lente.

6)
Si pensi di voler vedere tramite una lente il proprio pappagallo preferito e di volerlo
vedere diritto ma ridotto a un terzo della sua grandezza normale. Indicata con f la
distanza focale, determinare il tipo di lente necessario e le distanze dell'oggetto e
dell'immagine in funzione di f. Costruire un grafico dei raggi.
Se l'immagine deve essere diritta e rimpicciolita, dalla tabella [B] si ricava che la lente
deve essere divergente.
Dato che ,

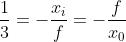
e quindi
, dove si deve tener presente che f<0


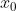
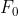
Sia che sono perciò positivi benché sia a destra e a sinistra della lente.
Essendo positivi è misurato a sinistra di e a destra di . Ne segue che
, mentre
Tutto ciò si può osservare nella sottostante figura.



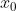
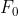
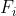
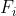

Per altra via,


7)
Una lente di vetro (ng = 1,5) sottile biconvessa ha raggi di curvatura di 30 e 60 cm.
Supposto di voler proiettare una immagine dimezzata di una lampada appesa al
soffitto su uno schermo di carta, quali devono essere le distanze lente-lampada e
lente-schermo? Costruire un grafico dei raggi.
Anzitutto per determinare la distanza focale si usa la equazione

II valore dell'ingrandimento trasversale è dato come 1/2, ma se si vuole che
l'immagine sia reale, esso deve essere negativo, quindi

Sostituendo questo valore nella equazione della lente sottile si ha

Nella sottostante figura, il diagramma dei raggi




Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





