



Chi presto giudica, presto si pente.
OTTICA TEORICA
SUPERFICI RIFRANGENTI SFERICHE (DIOTTRI)

SUPERFICI RIFRANGENTI SFERICHE (DIOTTRI)
Superfici sferiche esatte sono facili da costruire e quindi sono di grande interesse pratico.
La sottostante figura rappresenta una superficie sferica di raggio R e centro C (diottro).
Dalla pagina precedente si sa che un largo cono di raggi corrispondenti ad un segmento di
onda sferica propagantesi da S viene fatto convergere in P tramite un ovoide cartesiano.
Usando il principio di Fermat, si può dimostrare che, anche se la superficie è sferica, un
cono stretto di raggi converge in P.
In questo caso, con A vicino a V (cioè con ) si ha
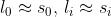
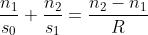
I raggi di questo tipo, che cioè formano con l'asse ottico angoli piccoli, sono detti parassiali.

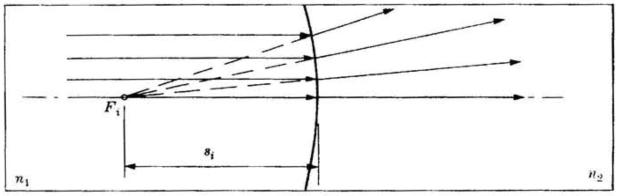
Vi è poi una particolare distanza dell'oggetto, , detta distanza focale dell'oggetto,
per la quale e le onde nel secondo mezzo sono piane, come mostrato nella sotto-
-stante figura. Sostituendo direttamente si ha
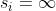


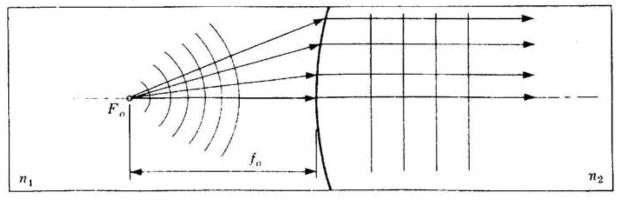
Analogamente, quando si assume abbiamo e risultano piane le onde
incidenti, come mostrato nella successiva figura. La distanza focale dell'immagine è
allora data da


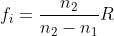
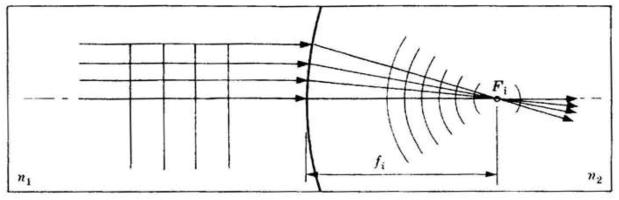
(FIG. A)
(FIG. B)
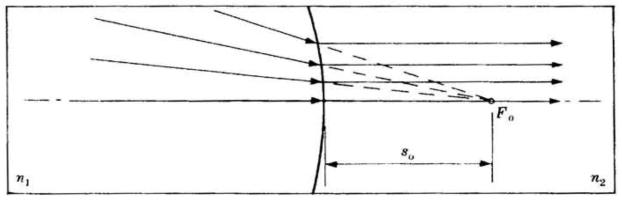
(FIG. C)
(FIG. D)
Si dice che un oggetto è reale quando la luce diverge da esso (fig. A) e che è virtuale
quando la luce converge verso di esso (fig. C). Analogamente si dice che una immagine
è reale quando la luce converge verso di essa (fig. B) e che è virtuale quando la luce
diverge da essa (fig. D).
Nella sottostante tabella sono riassunte le convenzioni di segno a cui ci atterremo in
queste pagine, in tutti i casi si assume che la luce provenga da sinistra.
Si noti che il segno meno per significa rispettivamente oggetto virtuale o
immagine virtuale.

Convenzioni di segno per superfici sferiche

+
a sinistra di V
+
a destra di V
R
+
quando C è a sinistra di V
+
sopra l’asse ottico
+
a sinistra di Fo
+
a destra di Fi
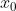




1 ) Si consideri una bacchetta di vetro (ng = l,50) circondata da aria con la estremità di
sinistra fissata ad una semisfera convessa di 2 cm di raggio. Se una sorgente
puntiforme si trova a 6 cm alla sinistra del vertice della semisfera, dove si trova la
sua immagine?
Essendo

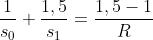
In questo caso , per cui
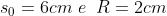
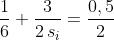

L'immagine è reale e si trova a destra di V nel vetro.

2) Si immagini che la bacchetta di vetro del precedente problema sia immersa in acqua
(nw = 1,33). Determinare la posizione dell'immagine della sorgente.
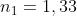

Ora mentre e quindi


oppure
Perciò cm . L'immagine è virtuale, a sinistra del vertice e la luce diverge
da essa.
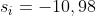
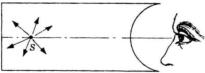

3) Si consideri il blocco di vetro raffigurato alla tua destra.
Se la sorgente puntiforme è situata a 30 cm dal vertice
della estremità emisferica e se quest'ultima ha un raggio
di 10 cm, determinare la posizione dell'immagine vista
dall'osservatore.
In questo caso



oppure
Perciò . Ne segue che t'immagine è virtuale, cioè i raggi divergono da
essa ed è posta 10 cm alla sinistra del vertice nel vetro
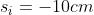


4) Si assume che la interfaccia di figura
a lato, abbia raggio di 5 cm e che separi
l'aria (sulla sinistra) dal vetro (ng = 1,5)
(sulla destra). Determinare fo e f;.
(Queste grandezze sono anche spesso
indicate rispettivamente come prima e
seconda distanza focale).
Per convenzione la luce arriva da sinistra; ne segue che
R , è positivo, è eguale a 5 cm. Da cui
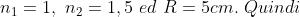
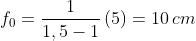
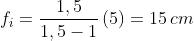


5)
Quale deve essere il raggio di curvatura della
estremità di destra della bacchetta di vetro
della figura a lato, se si vuole che il fascio di
raggi paralleli converga in un fuoco a 100 cm
dal vertice? La bacchetta di vetro (n = 1,46)
è immersa in alcool etilico (n = 1,36)
La distanza focale dell'immagine è data da
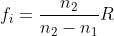

Il segno meno compare perché il centro di curvatura è a sinistra del vertice.


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





