



Chi ha meno ragione, grida più forte
OTTICA TEORICA
LE EQUAZIONI DI FRESNEL

LE EQUAZIONI DI FRESNEL
Circa 150 anni fa Augustin Jean Fresnel formulò un gruppo di equazioni che ci permettono
di calcolare quanta luce viene riflessa e quanta trasmessa attraverso una interfaccia.
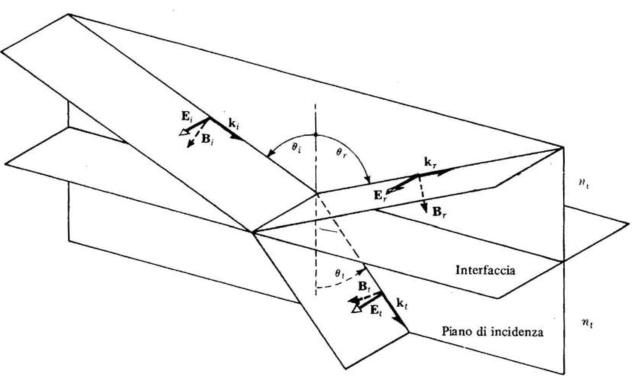
Si consideri un'onda luminosa piana armonica che colpisce l'interfaccia che divide due
dielettrici, con il campo E normale al piano di incidenza (vedi sottostante figura).
Le condizioni al contorno impongono di eguagliare le fasi delle onde incidente, riflessa e
rifratta (cioè
).
Ciò porta alle leggi di riflessione e di rifrazione già note. Ma esistono altre condizioni
al contorno per i campi E e B e queste portano alle equazioni di Fresnel. Indicando con
le ampiezze rispettivamente delle onde incidente, riflessa e rifratta, si ha
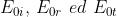
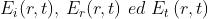
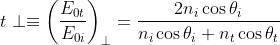
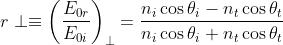
le espressioni cercate dei coefficienti di ampiezza rispettivamente di riflessione e di
rifrazione.
Eguagliando analogamente le condizioni al contorno nel caso di E parallelo al piano di
incidenza (si veda la sottostante figura), si ottiene un altro gruppo di coefficienti di
ampiezza:
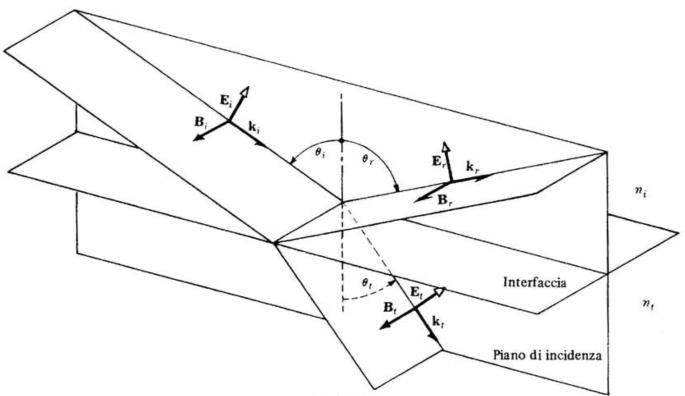
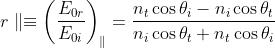
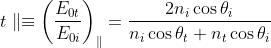
Oltre a questi rapporti tra le ampiezze dei campi, si può definire il potere riflettente R come
il rapporto tra il flusso (o potenza) riflesso e quello incidente e il potere trasmittente T come
rapporto tra il flusso trasmesso e il flusso incidente. In altre parole,
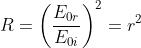
e
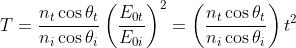
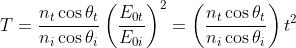
sono i coefficienti di potenza riflessa e trasmessa. Mentre R è semplicemente il
rapporto tra la intensità di radiazione riflessa e incidente, T ha un significato un po'
più complicato.
Ciò dipende dal fatto che la sezione trasversale del raggio trasmesso ha un 'area diversa da
quella degli altri due e mentre la potenza è indipendente dall'area della sezione del raggio,
la intensità di radiazione dipende anche da essa.

1 ) Riscrivere le espressioni dei coefficienti di ampiezza di riflessione come funzioni solo
di , liberarsi cioè dalla dipendenza esplicita di da .
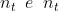
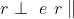
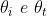
Cominciando dalla formula del coefficiente di ampiezza
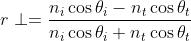
si divida per e si usi la legge di Snell ottenendo
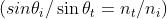
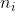
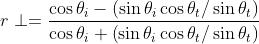
Questa espressione può assumere la forma più compatta
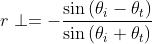
usando la identità
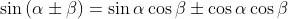
Analogamente
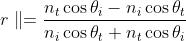
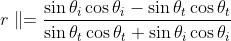
può essere riscritta come
usando la legge di Snell Ma quest'ultima equazione equivale a
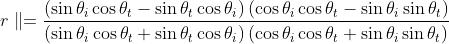
che a sua volta porta a
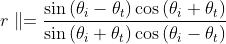
ed infine
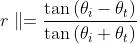
2) Ricavare delle espressioni per i coefficienti di ampiezza nel caso di incidenza
normale e calcolare i loro valori numerici relativi ad una interfaccia aria-vetro con
nt = 1,5.

Il dato caratteristico di questo caso è che
Quindi e
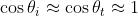
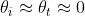
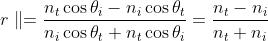
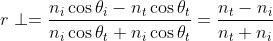
in sintesi

Nel caso di riflessione esterna su una interfaccia aria-vetro ,
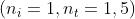
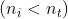
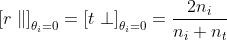
che nel caso aria-vetro assume il valore 0,8.

3) Esprimere i coefficienti di ampiezza di riflessione in funzione di .
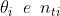
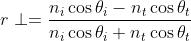
Partendo da
si divida per e si sostituisca ottenendo
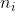
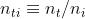
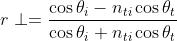
La legge di Snell può essere scritta come . Dato che
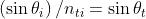
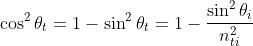
il coefficiente di ampiezza diventa
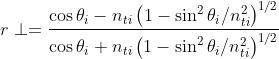
Più semplicemente
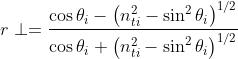
Analogamente
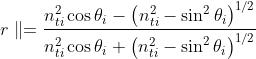

4) Determinare i valori dei coefficienti di ampiezza di riflessione per luce incidente a 30°
su una interfaccia aria-vetro,
= 1,50.
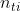
Da un precedente problema
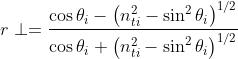
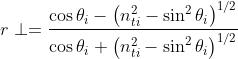
o, essendo cos 30° = 0,866 e sin 30° = 0,5,
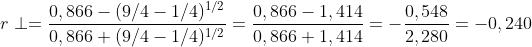
Analogamente
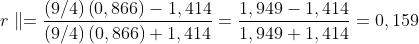
Il segno meno nel coefficiente perpendicolare significa che il campo riflesso ha verso
contrario a quello indicato in figura. In altre parole, la componente perpendicolare del
campo E dopo riflessione ha uno sfasamento di 180°.
5) Determinare il valore di
per luce incidente a 30° su una interfaccia aria-vetro,
e dimostrare che in questo caso .
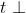
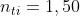

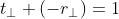
Usando la legge di Snell,
, si ha
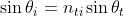
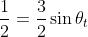
poichè
ne segue
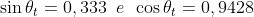
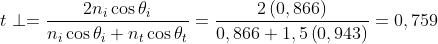
e, usando i risultati del problema 4),
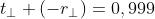
che ai nostri fini è abbastanza vicino a 1
L’equazione vale quale che sia il valore di mentre si ottiene
solo per .
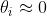
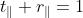
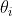
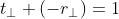

6) Si supponga che una onda polarizzata linearmente colpisca una interfaccia in modo
tale che il piano di vibrazione formi un angolo con il piano di incidenza. Ricavare
una espressione per il potere riflettente totale R, supponendo che il potere riflettente
per le componenti normale e parallela al piano di incidenza siano rispettivamente
.
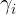
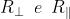
Dato che l'area delle sezioni trasversali dei raggi incidente e riflesso sono eguali, si
possono semplicemente considerare le corrispondenti intensità di radiazione. Ne segue
e quindi
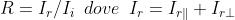
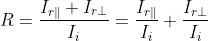
Dato che le componenti del campo sono esprimibili come
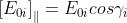
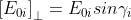
da segue che
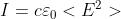
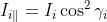
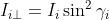
Sostituendo questi risultati nella espressione del potere riflettente si ottiene
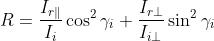
oppure
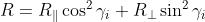
Il potere trasmittente ha la stessa forma:
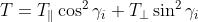

7) Ricavare una espressione (a) per il potere riflettente, (b) per il potere trasmittente nel
caso di incidenza quasi-normale. (c) Determinare la percentuale di luce persa per
riflessione ad una interfaccia aria-vetro (ng = 1,5)
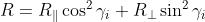
(a) Dal precedente problema
dove . Nel caso di incidenza normale, si ha che
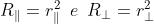
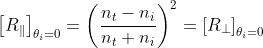
nel qual caso
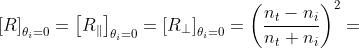
(b) Il potere trasmittente è dato da
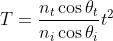
e il problema porta a
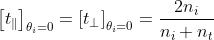
Quindi, ricordando che
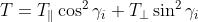
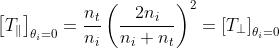
e
si ottiene
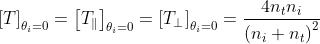
(c) Sostituendo nel risultato di (a) si ottiene nel caso di una singola
interfaccia aria-vetro una perdita di
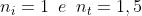
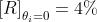

8) La luce naturale o non polarizzata è tale che l'angolo azimutale del problema 6)
cambia rapidamente e a caso, come l'ampiezza del campo. Ricavare una espressione
per , il potere riflettente della luce naturale, in funzione di , tenendo
presente che queste a loro volta sono entrambe funzione di .
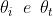
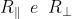
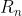
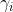
L'obiettivo è riscrivere
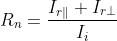
mettendovi dentro l'informazione che ci si sta occupando di luce non polarizzata
(tramite ).
Ritornando al problema 6), si noti che si sono determinati al solito modo,
elevando al quadrato e mediando sul tempo le componenti di campo. Ora però
è
una funzione del tempo e
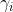
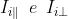
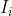
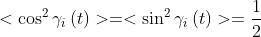
Quindi per la luce naturale e si può scrivere
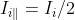
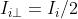
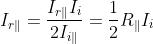
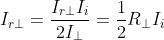
ne segue
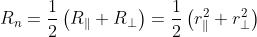

9) Dato un raggio di luce naturale che colpisce una interfaccia aria-vetro a
70° , qual è la percentuale della intensità di'radiazione incidente che viene riflessa?
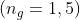
Dal precedente problema
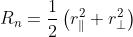
mentre dal problema 3) si ha
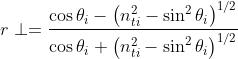
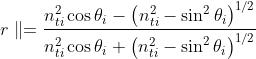
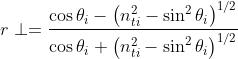
Con , si ha
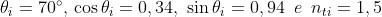
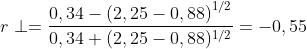
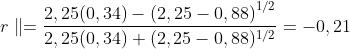
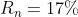
Sostituendo nella equazione del potere riflettente si ha


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





