



Commettere malvagità a favore del padrone è perfino considerato un merito.
OTTICA TEORICA

RIFLESSIONE E RIFRAZIONE

INTRODUZIONE
Questa sezione si occupa prevalentemente della riflessione su una interfaccia e del passaggio
della luce attraverso una interfaccia che divide due materiali diversi.
Almeno in teoria, si potrebbe usare il formalismo di Maxwell per definire il percorso di una
onda attraverso un mezzo, ma vi sono altri metodi in generale più semplici.
La legge di Snell, la legge della riflessione e il principio di Fermat - tutti di almeno trecento
anni fa - descrivono vari aspetti del comportamento della luce senza addentrarsi nella sua
reale natura.
Le equazioni di Fresnel vanno al di là della semplice determinazione della direzione del
percorso e permettono di calcolare la percentuale di luce riflessa e la percentuale di luce
trasmessa ad ogni interfaccia.
LE LEGGI DELLA RIFLESSIONE E DELLA RIFRAZIONE
La sottostante figura (a) rappresenta un'onda piana che arriva all'interfaccia tra due mezzi di
indici di rifrazione rispettivamente ni, e nt indietro nel mezzo da cui proviene, mentre
un'altra frazione si propaga nel secondo mezzo.
Quest'ultima frazione è detta onda rifratta.
Gli angoli si riferiscono rispettivamente alle onde incidente, riflessa e rifratta
(trasmessa). La sottostante figura (b) dà l'immagine dei raggi associata al fenomeno in
discussione. Un raggio è una retta avente la direzione del flusso di energia raggiante e in un
mezzo isotropo esso coincide con la normale al fronte d'onda. E' evidente che in un mezzo
del genere i raggi sono paralleli al vettore di propagazione dell'onda, k.

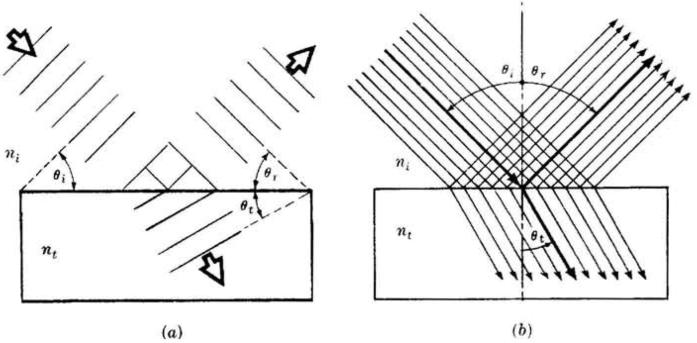
Le tre leggi fondamentali della riflessione e della rifrazione affermano che:
(1) I raggi incidente, riflesso e rifratto giacciono' tutti in un piano, detto piano di
incidenza, normale alla interfaccia.
(2) L'angolo di incidenza è eguale all'angolo di riflessione: .
(3) Le direzioni dei raggi incidente e rifratto sono legate dalla legge di Snell :



1 ) Un raggio di luce collimata (cioè a raggi paralleli) si propaga nell'aria e forma un
angolo di 30° con la normale ad una lastra di vetro. Determinare la direzione del
raggio che si trasmette nel vetro, sapendo che l'indice di rifrazione del vetro è .
La legge di Snell
,stabilisce la relazione esistente tra l'angolo di incidenza
e l'angolo di rifrazione. Nel caso in esame per l’aria, e ,per cui
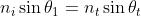
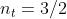

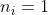


Dato che ,



e quindi
Questo è l'angolo formato con la normale, come indicato nella figura (b).

2) Si consideri la interfaccia tra due mezzi, uno vetro e l'altro acqua .
Un raggio che si propaga nel vetro colpisce la interfaccia con una inclinazione di 45°
e si rifrange nell'acqua. Determinare l'angolo di rifrazione.

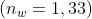
Si applica la legge di Snell
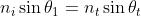
Il mezzo attraversato dal raggio incidente è vetro, . Ciò porta a


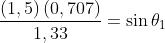
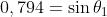
Ne segue


3) Determinare la relazione esistente tra , nel caso e nel caso .
Definendo l'indice di rifrazione relativo come , la legge di Snell
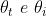
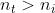




diventa
Se il secondo mezzo è quello a densità ottica maggiore, se cioè , allora
e
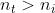

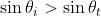
Dato che sia che sono compresi tra 0 e 90°,

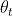

Analogamente, quando ,
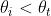


4) (a) Dimostrare che un raggio che colpisce con un angolo una lastra piana di vetro
immersa nell'aria, emerge dalla lastra con lo stesso angolo.
(b) Ricavare una espressione che dia lo spostamento a subito dal raggio in funzione
dello spessore d del vetro.


(a) Si deve dimostrare che in figura (A) . Per la legge di Snell si ha
dove . Inoltre sulla seconda superficie
Confrontando le due espressioni si ha
e quindi ; i raggi incidente ed emergente sono tra loro paralleli
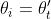


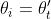

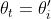
(b) Nella figura (b), e quindi nel triangolo CAD
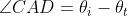

Ma , da cui deriva che

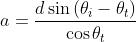

5) Si considerino due mezzi (rispettivamente di indice ) separati da una
interfaccia piana. Nel mezzo più deriso ( ) è collocato, a distanza y dalla interfaccia, un
oggetto. Un osservatore sopra l'interfaccia vedrebbe l'oggetto come se esso si trovasse a
distanza y' sotto di essa. Scrivere una espressione che dia y' in funzione di y e degli
indici di rifrazione, supponendo che la linea di visuale che unisce l'osservatore e l'oggetto
sia quasi normale alla interfaccia.
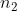
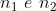
In figura (B) è data la geometria del problema.E’ noto che

e dalla figura si ricava che
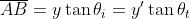
Dividendo membro a membro le due equazioni si ha
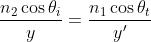
Dato che nel caso in esame e quindi anche sono piccoli, e

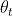

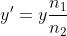
La espressione risulta assai più complicata quando ; non è piccolo.


6) A un pescatore un pesce sembra trovarsi 2 m sotto la superficie di uno stagno quasi
esattamente sotto di lui. A quale profondità si trova realmente il pesce?
In base al precedente problema . In questo caso y' = 2 m, n1 = 1 e n2 = 1,33.
Sostituendo nella equazione si ha che in realtà il pesce si trova alla profondità di



7) Si consideri un sistema costituito da strati sovrapposti di materiali trasparenti di
differente spessore. Dimostrare che la direzione del raggio emergente dal sistema è
funzione solo dell'angolo di incidenza e degli indici di rifrazione del primo e dell'ultimo
dei materiali costituenti il sistema ( ).

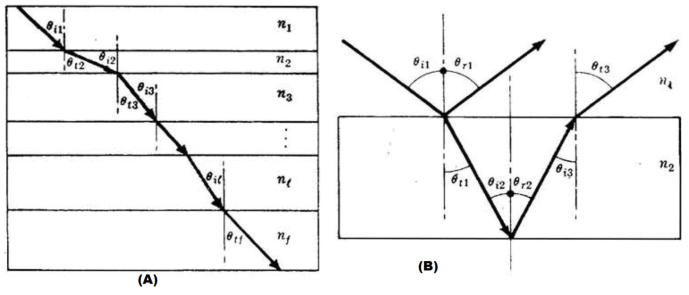
Facendo riferimento alla figura (A), per la Legge di Snell, si ha:
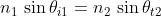

…………………………………

Dato che , da queste equazioni si ha
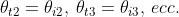
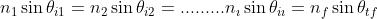
Da cui

Si noti che se come nel caso di una pila di lastre di vetro immerse nell'aria,
e i raggi incidente ed emergente sono paralleli.



8) Un raggio laser di luce collimata risplende su un serbatoio d'acqua. Una parte del
raggio viene riflesso dalla superficie dell'acqua e una parte dal fondo del serbatoio
come indicato nella soprastante figura (B). Dimostrare che i due raggi riflessi indietro
nel primo mezzo risultano paralleli.
Dato che gli angoli alterni interni formati da due rette parallele sono eguali, si ha

La legge della riflessione dice che

Quindi Dalla Legge di Snell, si ha


Sostituendo si ha
e quindi




Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





