



Mi dia una pomata per la distrazione al piede sinistro. (distorsione)
OTTICA TEORICA
INDICE DI RIFRAZIONE E INTENSITA’ DI RADIAZIONE

L'INDICE DI RIFRAZIONE
L'analisi teorica di Maxwell portava a prevedere per le onde elettromagnetiche una
velocità di propagazione nel vuoto .Invece un'onda che si propaga in un
mezzo materiale viaggia ad una velocità v = l/W, dove e sono la permettività e la
permeabilità del mezzo.
L'indice assoluto di rifrazione risulta quindi definito come
Generalmente le proprietà magnetiche dei mezzi hanno scarso effetto su
, dato che
nei materiali che interessano .
Una onda elettromagnetica che entra in un mezzo, applica ad esso un campo elettrico e
quindi il mezzo diventa elettricamente polarizzato. Ciò a sua volta ha effetto su
e, che poi
determina
. Tutto ciò dipende dalla frequenza dell'onda che colpisce il mezzo. La figura
sottostante mostra la dipendenza di dalla frequenza per varie sostanze di interesse
comune.
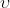

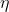
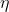
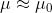
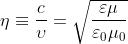
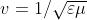
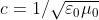

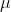

1)
Della luce avente nel vuoto lunghezza d'onda passa dal vuoto in un
diamante . Generalmente la frequenza resta costante quando la luce passa da
una sostanza ad un'altra. Assumendo che questo sia il caso, calcolare lunghezza d'onda
e velocità dell'onda nel diamante.
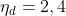
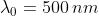
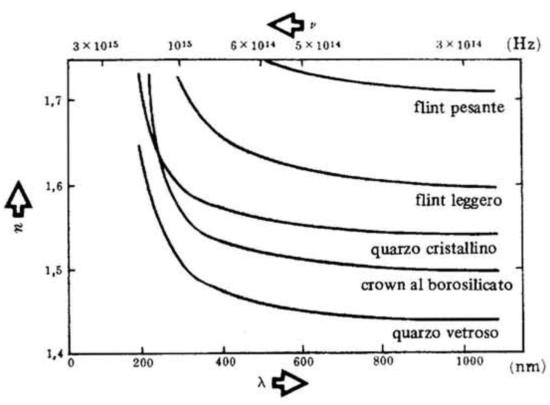
Dato che . Quanto alla lunghezz d’onda,
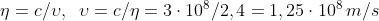
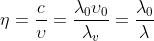
essendo . Quindi
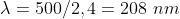
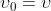

2) Si supponga che un'onda luminosa si propaghi dal punto A al punto B e si collochi
sul suo cammino una lastra di vetro di spessore
= 1 mm. Di quanto risulterà
alterata in B la fase dell'onda se = 500 nm?

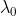
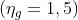
L'indice di rifrazione dell'aria (1,000293 a 0°C e 1 atmosfera) è assunto eguale a
uno. Il numero delle onde che si hanno nell'aria nel tratto
è La variazione di
fase associata è . Quando si inserisce nel percorso la lastra di vetro, si vengono
ad avere onde nell'aria e onde nel vetro. La differenza di fase è quindi
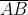
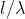
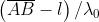
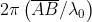
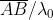
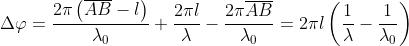
Ma e quindi ed in questo caso particolare:
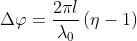
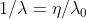
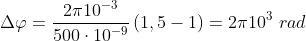

3) Un' onda armonica piana infrarossa che si propaga in un mezzo trasparente è data,
in unità SI come al solito, da:
Determinare l'indice di rifrazione del mezzo a quella frequenza e la lunghezza d'onda
della perturbazione nel vuoto

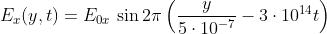
Riportandoci alla forma familiare per la fase k(y - vt) l'equazione data diventa
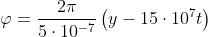
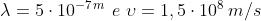
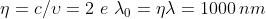
Evidentemente Quindi

4) Una radiazione luminosa proveniente da una lampada al sodio attraversa
un recipiente di glicerina (indice 1,47) lungo 20 m in un tempo t1. Supponendo che la
stessa radiazione impieghi un tempo t2 ad attraversare lo stesso recipiente pieno di
bisolfuro di carbonio (indice 1,63), determinare la differenza t2-t1
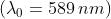
Dato che
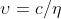
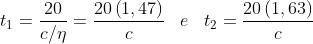
Ne segue
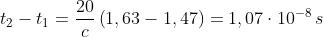
INTENSITA' DI RADIAZIONE
Un'onda luminosa che si irradia nello spazio alla velocità di 300 000 chilometri al secondo
porta energia elettromagnetica e quindi può interagire con un rivelatore, sia esso una
pellicola, una retina o una cellula foto elettrica. L'energia si trasmette nella direzione in cui si
propaga l'onda, cioè nella direzione di E x B. Ne segue che l'energia che nell'unità di
tempo colpisce perpendicolarmente l'unità di area di una superficie posta nello
spazio libero è data dal vettore di Poynting S, dove

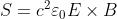
L'energia per unità di tempo è una potenza, per cui in unità SI S è espresso in .
Nel campo delle frequenze ottiche, E, B ed S oscillano tutti rapidissimamente e risulta
poco pratico cercare di misurare direttamente il valore istantaneo di S. Si determina invece
il suo valore medio (S) in un certo intervallo di tempo. A questo valore è dato il nome di
densità di flusso di radiazione.
Quando si tratta di energia che emana da una superficie, la densità di flusso è detta
potere emissivo; quando si tratta di energia che colpisce una superficie, la densità di
flusso è detta intensità di radiazione o illuminamento ed è indicata col simbolo .
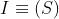
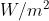

1 )
Un laser emette un raggio di 2 mm di diametro di luce altamente collimata ad una
potenza, o flusso raggiante, di 100 mW. Calcolare la intensità di radiazione,
supponendo totalmente nulla la divergenza.
La sezione trasversale del raggio è e quindi
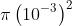
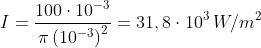

2) Un'onda elettromagnetica armonica che si propaga nel vuoto è data da
Dimostrare che
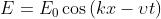
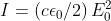
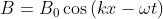
Il campo B ha la forma e quindi
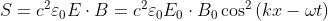
Ne consegue
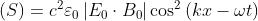
Calcolando la media in un intervallo di tempo T si ha
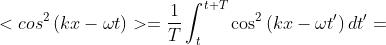
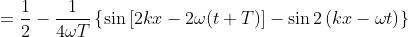
Quando . Ne segue che, essendo ,
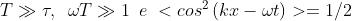
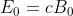
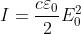
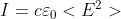
o, se si preferisce

3) Un'onda elettromagnetica piana che si propaga nel vuoto ha un campo E (detto anche
campo ottico) dato da Ex=0, Ey=0 e
Calcolare la densità di flusso corrispondente.
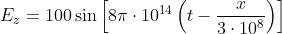
Da un precedente problema, Essendo
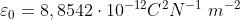
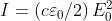
ed

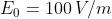
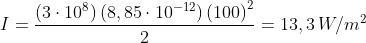

4) Si consideri un'onda elettromagnetica piana armonica che si propaga nello spazio
lungo l'asse delle y e si supponga che il campo E sia linearmente polarizzato nel piano yz
e che sia .Scrivere una espressione del corrispondente campo B nel caso in
cui l'intensità di radiazione sia .
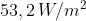
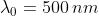
Dalla intensità di radiazione si può determinare Eo :
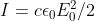
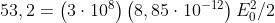
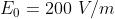
Allora, da si ha che
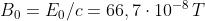
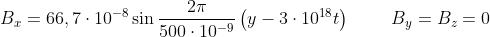

5) Una sorgente puntifonne monocromatica di 60 W irradia uniformemente in tutte le
direzioni nel vuoto e a 2,0 m di distanza è collocato un rivelatore. Determinare
l'ampiezza del campo E rilevata dallo strumento, sapendo che
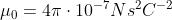
Se A è la superficie di una sfera di raggio r con centro nella sorgente e I è l'intensità
di radiazione a quella distanza, la potenza irradiata dalla sorgente è data da ,
o dalla espressione equivalente . Quindi
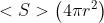
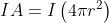
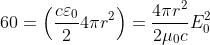
Ne segue che
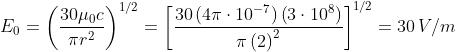


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





