



Non colpire mai un uomo con gli occhiali. Usa il tuo pugno
OTTICA TEORICA

FASE E VELOCITA’ DI FASE

FASE E VELOCITA' DI FASE
Uno dei concetti più importanti con cui avremo a che fare è la fase,
, di un'onda
armonica, che è per definizione semplicemente l'argomento della funzione seno:
La funzione d'onda nella forma usata finora rappresenta un caso particolare, dato
che per
.Ma non vi è alcuna ragione che impedisce che l'ampiezza
dell'onda assuma per
un valore qualsiasi. Ciò si ottiene facendo slittare la
funzione seno, mediante la introduzione di una fase iniziale
in modo che sia
Quando si osserva un'onda armonica che si propaga, per determinare la sua velocità di
propagazione, si studia il moto di un punto in cui l'ampiezza della perturbazione resti
costante. Per un tale punto anche la fase deve restare costante; ne segue che la velocità di
propagazione dell'onda è la velocità alla quale si sposta la condizione di fase costante, vale
a dire
La grandezza positiva v, che è la velocità di propagazione di una onda armonica, è
detta anche velocità di fase.








1)
Si disegni il profilo dell'onda , dove la fase iniziale è di volta
in volta .


Per . Dividendo l'asse x in intervalli di , si ottengono
i profili riportati in figura:

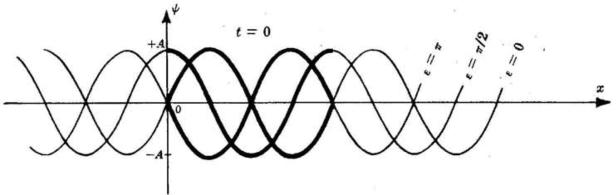
Se si stesse parlando di una onda generata lungo una corda dalla azione della
mano in x = 0, lo spostamento iniziale (t=0) sarebbe verso il basso (rispetto allo
zero) per
e verso l'alto per



2) Qual è il valore della funzione d'onda in x = 0 per
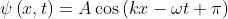
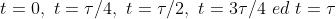
?
Sostituendo direttamente in si ha
inoltre, dato che e quindi

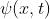
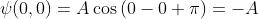


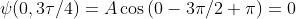

Analogamente

3)
Esaminando la fase, determinare la direzione del moto delle onde progressive
rappresentate da

La condizione di fase costante, cioè
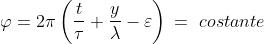
comporta che y sia in diminuzione, dato che t è positivo e crescente. In altre parole,
affinché
sia costante deve essere un'onda che si propaga nella direzione delle
y negative . Analogamente, è un'onda che si propaga nella direzione delle z
crescenti o positive. Il segno di
è irrilevante ai fini della direzione del moto.


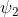
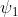

4) Scrivere una espressione analitica del profilo (per t=0) di un'onda armonica, che si
propaga nella direzione delle x positive, tale che per x=0, = 10; per x= = , =20; e
per , =0.
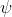

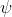

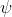
Dato che . Sostituendo in questa espressione i dati si ha
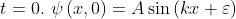



Combinando le prime due espressioni si ottiene
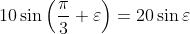
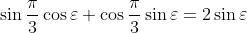

oppure
da cui
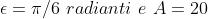
Quindi .
Quindi


5) Data un'onda che si propaga con profilo costante nella direzione delle x positive alla
velocità v, ci si può aspettare che . (Questo equivale
semplicemente ad affermare che un punto dell'onda avente una data fase percorrerà
la distanza nel tempo .) Dimostrare che la funzione d'onda soddisfa a
questa condizione.
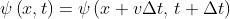





Sostituendo e a t, la funzione d’onda assegnata diventa
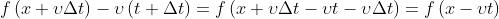


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





