



A parole essere delle brave persone non è poi cosi difficile
OTTICA TEORICA


MOTO ONDULATORIO

INTRODUZIONE
L’ottica e lo studio della luce o, più generalmente, lo studio dello spettro elettromagnetico.
Ai fini della nostra trattazione, daremo un rilievo particolare agli aspetti ondulatori
della luce. Tuttavia, benché la luce era un fenomeno elettromagnetico, e possibile
studiare gran perte dell’ottica senza specificare di quale tipo di onde si stia parlando.
L’ampia opera di Fresnel ( l788- t827), così utile ancora oggi, fu ad esempio compiuta sulla
base del modello del mezzo elastico, modello oramai da lungo tempo abbandonato.
L’EQUAZIONE DIFFERENZIALE DELLE ONDE
Una semplice onda che si trasmette lungo una corda ha molte proprieta in comune con
un’onda luminosa. Lo spostamento della corda è perpendicolare alla direzione
di propagazione della perturbazione, ciò vale a dire che l’onda st propaga lungo la corda,
mentre ogni singolo elemento della corda non fa che muoversi di moto alternativo intorno
alia sua posizione. Le onde di questo tipo sono dette trasversali.
La luce e appunto una onda trasversale, con i campi elettrico e magnetico variabili
in direzioni perpendicolari alla direzione di propagazione dell’onda stessa.

L’equazione differenziale delle onde :

descrive i fenomeni di questo genere (quando si ha una sola variabile spaziale). La
grandezza , detta funzione d’onda, rappresenta la perturbazione nello spazio
(x) e neI tempo (t), era che si tratti dello spostamento dei punti di una corda o
dell’ampiezza di un campo. Nell’equazione v è la velocity di propagazione dell’onda.
Una soluzione della equazione differenziale delle onde ha la forma


dove f è una funzionc della variabile (x-vt) dotata di derivata seconda e per il
resto arbitraria. In altri termini, (x-vt) può comparire al quadrato, al cubo o in
quale altra forma si voglia, a condizione che però compaia sempre come un tutto
unico. La forma della perturbazione, il suo profilo, si ottiene “fotografando” la
funzione d’onda in un dato istante. In termini matematici, ciò equivale ad assegnare
a t un valore cost ante; per esempio, per t = 0,

é il profilo. Cost se f(x) è la forma di uno scotimento impresso a una corda, f(x-vt)
descrive lo scotimento che si sposta nella direzione delle x positive alla velocita v .
Analogamente, g(x + vt) é una soluzione dell’equazione delle onde relativa ad un arbitrario
profilo g(x) che si propaga nella direzione delle x negative.


PROBLEMI RISOLTI
1)
Dimostrare che f(x-vt)
rappresenta una onda progressiva che si propaga nella
direzione delle x positive mantenendo immutato il profilo.
Si consideri un sistema di coordinate s’ che
si sposta verso destra assieme alla perturba-
-zione con velocità v come indicato in figura.
Nell’istante t= 0 i due sistemi di riferimento
s e s' sono sovrapposti per cui x’=x-vt.
Nel sistema s’ la funzione d’onda é indipe-
-ndente dal tempo. Ne consegue che in s'
il profilo resta fisso e la funzione d’onda
é data da

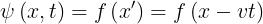
2)Dimostrare che è una soluzione delI’equazione differenziale
delle onde a una dimensione.
Sia f una funzione di x’ dove
a sua olta è una funzione di x e di t.
Usando la regola di derivazione delle funzioni composte,



e

e quindi

mentre

ne segue

ossia

3)Dimostrare che se e sono entrambe soluzioni dell’equazione
differenziale delle onde, anche + é una soluzione.
Dato che e sono soluzioni dell’equazione differenziale delle onde si ha:
Sommando membro a membro si ha
Il risultato ottenuto é detto principio di sovrapposizione per l'equazione differenziaIe delle
onde a una dimensione. Ne segue che
é la soluzione generate dell’equazione.











4) Dato il profilo

(a) Ricavare la espressione della onda progressiva corrispondente che si propaga
nella direzione delle y positive alla velocity di 2 m/s.
(b) Disegnare il profilo corrispondente a t=0 ed a t=1s.
a)
Basta sostituire y con o, nel caso particolare, con y - 2t. Quindi


b) si veda la sottostante figura



Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor




