



Quando il pidocchio casca nella tramoggia, crede d'essere il mugnaio
TECNOLOGIE ELETTRONICHE


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!
LE INDUTTANZE - Coefficiente di Autinduzione [A]
Coefficiente di Autoinduzione
CASO IDEALE DI UN CONDUTTORE CILINDRICO
RETTILINEO INDEFINITO
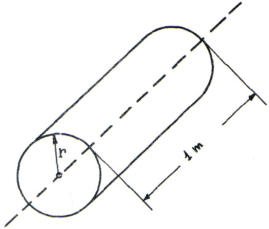
Caso ideale di un conduttore cilindrico rettilineo inde-
-finito in cui si suppone convogliata una corrente I
costante ed uniformemente ripartita nella sezione.
Come ìndica la sottotante figura, si consideri un metro
lineare di conduttore ed il flusso esterno di induzione Ф
con esso concatenato.
Per la relazlone Фc =L I, l'induttanza che il flusso consi-
-derato conferisce al conduttore e' data dall’ espressione
[1]

Indicando, alla distanza x dall'asse del conduttore, con
Hx ed lx rispettivamente il valore del campo magnetico
e la lunghezza della linea di forza del campo magnetico,
e' noto che:
da cui : [2]
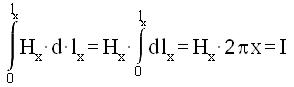

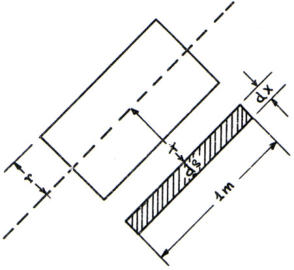
Con riferimento alle notazioni di cui alla figura
alla tua destra, indicando con Bx il valore della
induzione magnetica alla distanza x, con la
permeabilità' magnetica dell'aria e con dФ0 il
flusso elementare attraverso la superficie infini-
-tesima dS =- l dx , possono scriversi le relazioni:



ed indicando con a il valore di x in corrispondenza del
quale il campo magnetico può' ritenersi praticamente estinto, integrando tra i limiti x=r ed
x=a l'ultima relazione si ottiene:
e per la relazione [1] [3]
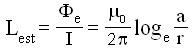



Com'è noto nell'interno del conduttore ed in ciascuna sezione di
questo le linee di forza del campo magnetico si mantengono come
all'esterno circolari.
Con riferimento alla figura a sinistra e sempre supponendo
uniforme la distribuzione della corrente nel conduttore, indicando
con Ix la corrente convogliata attraverso l'area circolare di raggio
x, dalla relazione:
si ottiene


Con riferimento alla distribuzione del campo magnetico
all'interno del conduttore la relazione ∫H dl = NI deve essere
scritta nella forma:
da cui: ed
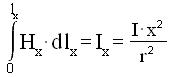

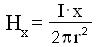
Di conseguenza il flusso di induzione dФx che attraversa una generica superficie
elementare dS = l dx e' espresso dalla relazione:

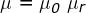
essendo : la permeabilità' magnetica del conduttore.
Poichè i flussi di attraverso le diverse aeree infinitesime si concatenano con correnti di
diverso valore l'induttanza Li dovuta alla distribuzione del flusso all'interno del conduttore
non può' essere ottenuta, come nel caso precedente dividendo per I il risultato ottenuto
dall'integrazione della relazione [2].
D'altra parte può' dirsi che un flusso dФi. concatenato con una corrente Ix = (I x2 / r2)
equivale ad un flusso concatenato x2/r2 volte con la corrente I.
In altri termini,agli effetti del calcolo della induttanza interna Li, anziché' il flusso dФx
dovrà' essere considerato il flusso elementare:

Integrando tra i limiti x=0 ed x=r la soprastante relazione, si ottiene:
ed inoltre
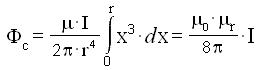
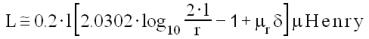
Tenendo conto della relazione [3], l'induttanza totale L relativa ad un tratto l di conduttore,
espresso in metri, e' data dalla relazione:

od anche, essendo:




Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor









