



I grandi amori si annunciano in modo preciso. Appena la vedi dici: chi è questa stronza?
TECNOLOGIE ELETTRONICHE


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!
I Condensatori - Le Perdite




Perdite nei condensatori
Le perdite di potenza nel dielettrico del condensatori
sono dovute sia al fatto che la resistività di questo
non può essere necessariamente infinita, sia per il
fenomeno di isteresi, dielettrica che si verifica quando
tra le armature del condensatore e' applicata una
tensione alternata .
Fanno eccezione l'aria secca ed il vuoto che non
presentando isteresi restituiscono interamente
l'energia spesa per la polarizzazione.
Come e' noto, l'induzione elettrica
di un
isolante e' eguale alla somma della polarizzazione
specifica p e della induzione che si avrebbe
nello spazio vuoto a parità di campo elettrico E, ossia:


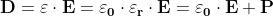

[2]
[3]
essendo:
la suscettibilità dielettrica

Se il campo elettrico varia con legge sinusoidale:
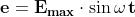
anche la polarizzazione P varia con la stessa legge. Mentre nel vuoto l'induzione Do e quindi
la polarizzazione che con questa si identifica assume immediatamente il valore che corrispo-
-nde ad un certo valore e del campo, per gli altri dielettrici la polarizzazione segue con rita-
-rdo, le variazioni del campo elettrico. Può' quindi in questo caso scriversi la relazione :
essendo t1 il tempo di ritardo
ne consegue :
che sviluppando la relazione :
e per la [2] si ottiene :
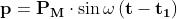




Sviluppando la soprastante relazione, si ottiene:

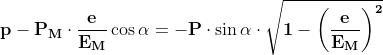
ed elevando a quadrato ambo i membri dell'equazione
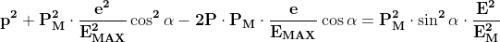

da cui :

Mancando i termini di primo grado in p ed e la soprastante
equazione rappresenta un'ellisse riferita al centro degli assi
cartesiani.
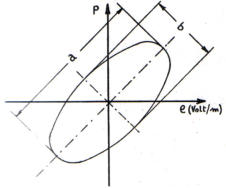
Il ciclo di isteresi dielettrica e' rappresentato dalla ellisse
indicata nella figura a lato.
E' facile dimostrare che l'energia dissipata in un periodo e per
unita' di volume e' rappresentata dall'area dell'ellisse.

Supponendo infatti che il campo elettrico sia uniforme , l'energia necessaria per polarizzare,
con una d.d.p. costante v, della quantità' di elettricita' Q un parallelepipedo di dielettrico
disposto nel campo elettrico come indicato nella sottostante figura, e' data dalla relazione:


ed essendo

risulta
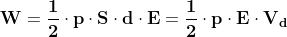
essendo Vd il volume del dielettrico e l'energia per unità di volume

Una variazione elementare dE di campo elettrico porta in conseguenza ad una
variazione dP di polarizzazione e quindi ad una variazione di energia:

ma essendo per la relazione [3] :
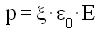
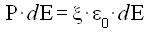
si ha :
ossia essendo :
e l'energia relativa ad un intero ciclo

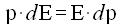

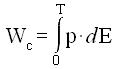
Rimane così dimostrato che l'area del ciclo di isteresi rappresenta il lavoro compiuto dal
campo elettrico per far percorrere all'unita' di volume di dielettrico, un ciclo di polariz-
-zazione, ossia l'energia trasformata in calore per unita' di volume e per ciclo.
L'area del ciclo di isteresi può' essere valutata o graficamente o per mezzo della relazione :
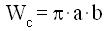
una volta che siano conosciuti i valori "a"e "b" dei semiassi dell'ellisse. A tale scopo ponendo
la relazione [4] nella forma

i valori di
possono essere calcolati in base alle note relazioni :
da cui :
[5]
ed avendo posto:

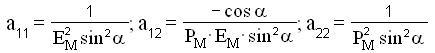
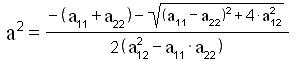
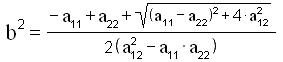

si ottiene:


ed essendo:


si ha quindi per la relazione [5]
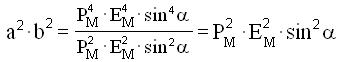
da cui:

Essendo per l'aria e per il vuoto , la soprastante relazione conferma che questi
dielettrici sono privi di perdite.
Lo studio teorico che attribuisce al ciclo di isteresi dielettrica una forma ellittica trova
una conferma sperimentale per gli isolanti di più' comune impiego.
Fanno eccezione, come osserveremo ad esempio, nello studio delle ceramiche al
titanato di Bario, solo alcuni particolari dielettrici, e la natura dei fenomeni che
possono determinare uno scostamento della forma del ciclo di isteresi dall'ellisse
teorica e' piuttosto complessa.
Una giusttflcazione di tale comportamento può' essere data, pensando che l'angolo
non si mantenga costante entro il periodo della tensione applicata.




Nell'impiego dei condensatori elettrostatici in c.a. le varie
perdite provocano una trasformazione di energia elettrica in
calore.
Come indica la figura alla tua sinistra,la corrente I, a causa di
una certa richiesta di potenza attiva e sfasata rispetto alla
tensione applicata alle armature in anticipo di 90° a meno di
un angolo δ detto di perdita il cui valore e' tanto più elevato
quanto maggiore e' l'entità' delle perdite.
Poiché' in definitiva le varie perdite provocano un riscaldamento del dielettrico e' convenzio-
-ne tenerne conto, come se questo fosse dovuto ad una resistenza R risposta in parallelo
alla capacita'.
Con riferimento al sovrastante circuito equivalente, si ha :
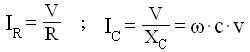
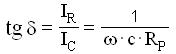
da cui:
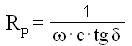
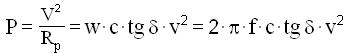
essendo f la frequenza lavoro.

Tenendo poi conto della resistenza e della induttanza dovute ai terminali ed
alle superfici delle armature il circuito equivalente diviene come quello rappre-
-sentato a lato.
Mentre nell'impiego in corrente alternata sarebbe desiderabile che un conden-
-satore si comportasse a qualsiasi frequenza, come una reattanza capacitiva
pura, in pratica si tratta di una impedenza completa; può quindi avvenire che
in un certo campo di frequenza si comporti come una induttanza ed in un altro
come una capacita'.
Per ciascun condensatore esiste inoltre una frequenza di risonanza in corrispondenza della
quale l'impedenza si riduce ad una semplice resistenza.
Nella sottostante tabella e' riportato l'ordine di grandezza della frequenza di risonanza per
alcuni valori della capacità nominale.
Il valore delia differenza di potenziale che da' luogo alla perforazione del dielettrico e' in
stretta relazione con la distanza che separa le armature e la rigidità'dielettrica dell'isolante
impiegato.
Si definisce rigidità' dielettrica l'intensità' di un campo elettrico uniforme capace di
perforare il dielettrico.
I valori indicati, per essa, nei manuali, per i diversi materiali isolanti devono essere intesi,
come indicativi degli ordini di grandezza, polchè in pratica il valore della rigidità e' influen-
-zato da numerosi fattori, quali ad esempio impurità , condizioni ambientali, spessore del
provino, durata e modalità di applicazione della tenslone.
Nell'impiego in c.a. la rigidità si riduce con il diminuire della frequenza e della durata
della tensione applicata.
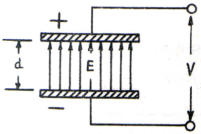
Se il condensatore è piano ed il campo elettrico può essere
considerato uniforme, come in quello rappresentato a lato,
campo elettrico e tensione applicata sono legati dalla relazione

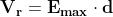

La tensione di rottura e' deducibile dalla soprastante relazione,
stabilendo per E il valore che corrisponde alla rigidità' dielettrica dell'isolante, ossia:

In pratica, per ragioni di sicurezza la tensione massima di lavoro e' fissata inferiore
almeno alla meta' della tensione di rottura.
Desiderando ridurre a parità di capacita' e tensione di lavoro la superficie delle armature e
lo spessore del dielettrico, allo scopo di diminuire le dimensioni di ingombro, e' necessario
impiegare isolanti che siano caratterizzati da elevati valori sia della rigidità' sia della costa-
-nte dielettrica relativa.
Quando un condensatore è impiegato in corrente continua, le perdite di energia dovute alle
correnti di dispersione una volta che sia rimossa la sorgente di alimentazione, fanno si' che
l'energia immagazzinata non si conservi indefinitivamente.
La resistenza di dispersione cui devesi attribuire l'inconveniente citato, e' indicata norma-
-lmente in MΩ e può'essere determinata misurando la costante di tempo RC durante la
scarica naturale; il suo valore può' variare per i diversi tipi da qualche secondo a diversi
giorni. La conoscenza del valore della resistenza di isolamento e' di particolare interesse
in ogni caso, ma soprattutto quando si debba dare un giudizio sulla possibilità' di impiego
di un condensatore in un circuito di memoria.
Per uno stesso condensatore le correnti di dispersione aumentano con la temperatura.
Anche il valore della capacita' varia con la temperatura. In modo analogo ai resistori
si definisce coefficiente di temperatura l'espressione

Vari autori preferiscono esprimerlo in parti per milioni e per grado centigrado [ppm/°C] .
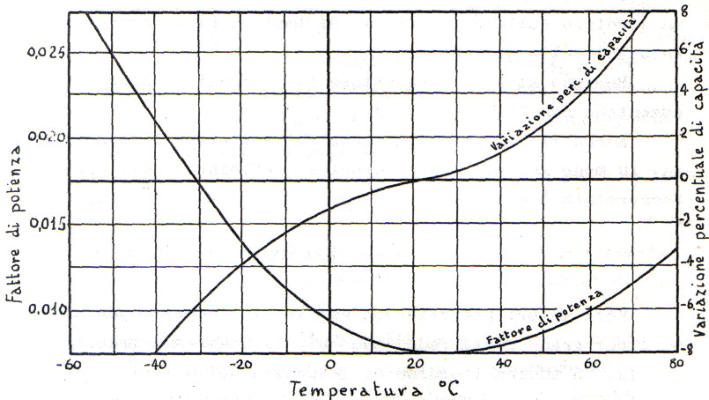
Il soprastante diagramma indica l'ordine di grandezza delle variazioni della capacita' e del
fattore di potenza in funzione della temperatura per condensatori a carta di uso generale.
I materiali dielettrici più' comunemente impiegati per la fabbricazione dei condensatori
possono essere distinti in 7 classi principali:

Mica,vetro e ceramiche a bassa perdita
Per valori di capacità sino a qualche centinaio di pF
Ceramiche ad elevata costante dielettrica
Per valori di capacità sino a qualche decina di nF
Carta
Per capacità da qualche migliaio di pF a diversi uF
Ossidi di metallo
Condensatori elettrolitici
Dielettrici sintetici (polistirene, polietilene, ecc.)
Per capacità da qualche centinaio di pF a diversi uF
Dielettrici liquidi
Condensatori ad alto isolamento
Aria
Condensatori variabili



Tipo di isolante
Costante dielettrica relativa
εr
Rigidità Dielettrica
Kv/cm
Carta
1,6 - 1,7
60 - 110
Carta bachelizzata
5
50 - 150
Carta paraffinata
2,5 - 4
400 - 500
Celluloide
2 - 7
100 - 300
Colofonia
2,5 - 2,8
100
Ebanite
2 - 3
60 - 250
Fibra
3,4 - 5
25 - 100
Gomma vulcanizzata
3 - 4,5
150 - 250
Mica
5 - 6
60 - 1200
Micalex
7 - 3
130 - 150
Micanite
3 - 4
200 - 480
Mylar
3
-
Nylon
3,5
-
Olio
2 - 2,6
100 - 160
Ossido di Tantalio
11
-
Paraffina
2 - 2,5
140 - 150
Plexiglass
3,5
-
Pyrex
4,7
-
Porcellana
4,5 - 16
210 - 600
Polistilene
2,5
-
Prespan
2,5 - 5
7 - 120
Polietilene
-
-
Teflon
2
-
Titanato di Bario
6000
-
Quarzo fuso
4,4
-
Vetro
4,5 - 10
100



Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor









