



Le droghe non ti portano da nessuna parte... ma almeno è una strada panoramica
Radiotecnica

..può sembrare che la tecnica abbia
poco valore, ma è solo l'illusione di
chi la acquisisce e la adopera,
sapendone poco o niente.....




OSTACOLI DI SPESSORE FINITO E OSTACOLI MULTIPLI
Ostacoli di spessore finito
In molte situazioni reali, particolarmente nei collegamenti con
mezzi mobili, il problema dell’ostacolo presenta una rapprese-
-ntazione geometrica del tipo di quella mostrata nella sotto.
-stante figura.
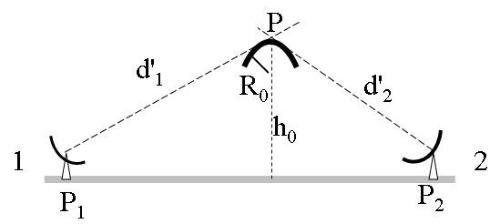
L’ostacolo ha spessore finito.
Assumiamo come tondeggiante la sua parte superiore, approssimabile ad una semicirconfe-
-renza di raggio Ro (in una rappresentazione bidimensionale).
Si traccino le tangenti a tale semicirconferenza passanti per le posizioni delle due antenne
(P1 e P2) e sia P il punto di intersezione di tali tangenti.
Come primo passo, si calcola il fattore di diffrazione (in dB) per un ostacolo laminare
equivalente.
Si usa la trattazione delle precedenti pagine. Supponendo di avere v1 > 2.4, si ha:
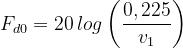
con
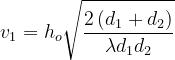
sono i parametri che avrebbe un ostacolo laminare perpendicolare alla
congiungente tra le due antenne ed esteso fino al punto P.
Esistono contributi aggiuntivi , dovuti a riflessioni e perdite lungo la propagazione
superficiale.
Per il loro calcolo, si usano semplici formule algebriche ottenute come approssimazioni di
modelli teorici.
L’ Unione Internazionale delle Telecomunicazioni suggerisce la seguente procedura.
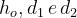
•
Si calcola
•
Si calcola
•
Il fattore di diffrazione totale è dato da:
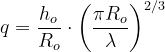
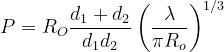
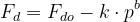
dove
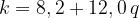
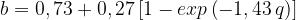
Il problema dell’ostacolo multiplo
In generale, tra le due antenne saranno presenti numerosi ostacoli. Per tenerne
conto, sono state sviluppate alcune teorie che stimano il fattore di diffrazione comples-
-sivo, utilizzando opportunamente la teoria del singolo ostacolo.
Se ne riportano in seguito alcune tra le più note.
Il metodo di Deygout
Siano presenti un numero N di ostacoli tra le due antenne (N = 3 nell’esempio riportato
nella sottostante figura).
Per ciascun ostacolo si calcola il fattore di diffrazione che si avrebbe se fosse l’unico
presente.
Si usa il metodo descritto nelle precedenti pagine.
Per il generico ostacolo i-esimo, indicando con il valore assunto dal parametro
per
quell’ostacolo, si procede in due passi.
1.
Si calcola con la:
2.
Si calcola il fattore di diffrazione usando le formule già enunciate in precedenza.
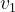
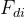
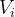
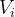
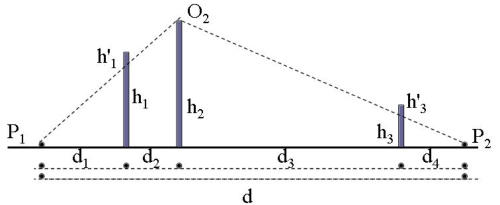
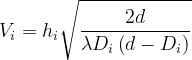
è l’altezza dell’ostacolo, d è la lunghezza totale del collegamento e è la
distanza dell’ostacolo i-esimo dall’antenna trasmittente
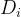
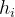
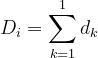
D’ora in avanti, si userà la notazione:
Sia m il valore di i per cui è massimo (ostacolo principale).
Nell’esempio della soprastante figura, si ha m = 2, con:
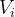
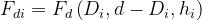
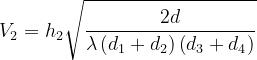
Si considerano, successivamente, i due subcollegamenti tra il bordo dell’ostacolo
principale ( nell’esempio della soprastante figura) ed i due punti .
Per ciascuno dei due subcollegamenti, si determinano i nuovi ostacoli principali
e si calcolano i nuovi fattori di diffrazione parziali .
Si procede poi iterativamente, calcolando i fattori dell’iterazione successiva, fino ad
esaurire tutti gli ostacoli.
Alla fine si sommano (in dB) i fattori di diffrazione parziali.
Nell’esempio della figura di cui sopra, essendo N = 3, sono sufficienti le prime due
iterazioni.
Si ha: .
Il fattore di diffrazione totale sarà dato da:
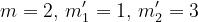
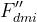
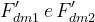
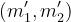
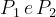
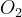
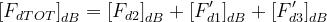
dove
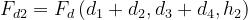
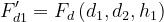
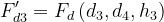
Il significato dei parametri h può essere dedotto dalla figura di riferimento.
Nei passi successivi al primo, si può sempre supporre che le distanze oblique siano
approssimabili con le loro proiezioni orizzontali:
Il metodo di Deygout tende a sovrastimare l’effetto complessivo quando sono presenti
numerosi ostacoli e/o alcuni di essi sono collocati a distanze relativamente piccole.
Per ovviare a questo problema, è stato introdotto un fattore correttivo dovuto a
Causebrook.
Per semplicità, si farà riferimento direttamente al medesimo .
Si ha:
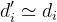
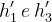
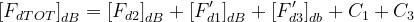
dove
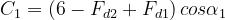
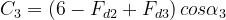
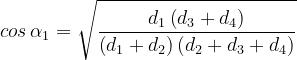
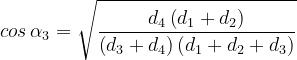
Il metodo di Giovaneli
Analogamente al metodo di Deygout, anche quello proposto da Giovaneli si basa sul
concetto di ostacolo principale.
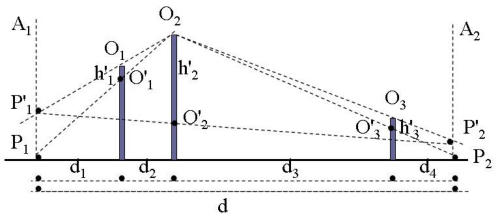
Per semplicità, facciamo riferimento allo stesso caso a tre ostacoli come mostrato nella
sottostante figura:
Si considerino i piani A1 e A2 passanti per i punti P1 e P2 e ortogonali alla direzione
del collegamento .
Si determinano l’ostacolo principale (m = 2 nel caso della soprastante figura) e gli ostacoli
principali dei subcammini ( della stessa figura).
Dal bordo superiore dell’ostacolo principale ( nel caso della precedente figura) si trac-
-ciano le semirette passanti per i punti superiori degli ostacoli principali dei subcammini
( nel caso della precedente figura).
Siano i punti di intersezione con i piani .
Si ottiene il punto come intersezione tra l’ostacolo principale e la congiungente .
Si ottengono i punti come intersezioni tra gli ostacoli 1 e 3 (rispettivamente) e la
congiungente .
Si definiscono:
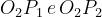
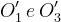
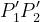
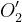
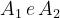
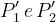
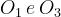
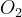
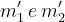
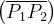
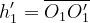
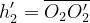
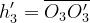
Il fattore di diffrazione totale, secondo l’algoritmo di Giovaneli, è dato (in dB) da:
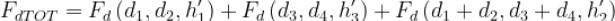
Se sono presenti ulteriori ostacoli oltre al principale e i due sub-principali, saranno
caratterizzati da franchi positivi rispetto alle semirette passanti per ,
ovvero per .
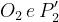
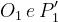
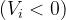
Effetti delle pareti
La crescente diffusione dei collegamenti con mezzi mobili rende molto attuale il
problema degli effetti che le pareti di edifici provocano sulle onde elettromagnetiche.
Sia data una parete, come mostrata in figura, che, in una
prima approssimazione semplificativa, assumiamo come
uno strato di spessore ∆t riempito di dielettrico uniforme
di costante dielettrica
.
Supponiamo che incida un’onda piana con angolo di
incidenza θ1.
Una frazione della potenza sarà riflessa dalla parete mentre
un’altra frazione (complementare alla precedente se è
reale) sarà trasmessa nel semispazio 3, aldilà della parete
stessa.
Il problema ha interesse applicativo, nelle comunicazioni con
mezzi mobili, per numerosi motivi.
•
La riflessione ha interesse per stimare la propagazione in
ambiente urbano attraverso riflessioni multiple dalle facciate di edifici.
•
La trasmissione è importante qualora il terminale mobile sia collocato all’interno di un
edificio. Inoltre, consente di valutare il contributo all’illuminazione di una copertura
dovuta a propagazione attraverso gli edifici.
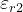
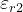
Con riferimento alla soprastante figura si ha:
1.
Mezzo 1: semispazio riempito di aria con costante dielettrica , impedenza del
mezzo .
2.
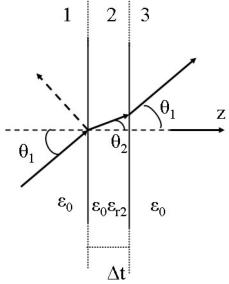
Mezzo 2: strato dielettrico di costante dielettrica
, impedenza del mezzo
3.
Mezzo 3: semispazio di proprietà analoghe a quelle del mezzo 1
Un’onda incidente da mezzo 1 con angolo sarà in parte riflessa, in parte trasmessa nel
mezzo 2 con angolo .
Per la legge di Snell:
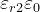
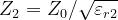
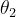
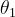
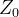
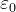
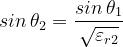
In corrispondenza dell’interfaccia tra mezzo 2 e mezzo 3, una parte della potenza
sarà trasmessa nel mezzo 3 (dove riprenderà a propagarsi con angolo ), un’altra sarà
riflessa.
All’interno del mezzo 2 saranno presenti riflessioni multiple e, se la è complessa,
dissipazione.
Se il mezzo 2 fosse un semispazio infinito i coefficienti di riflessione all’interfaccia 1-2
sarebbero dati da:
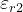
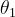
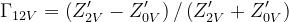
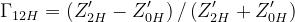
(polarizzazione verticale, o TM)
(polarizzazione orizzontale, o TE)
dove
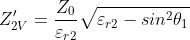
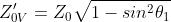
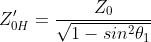
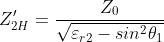
I coefficienti di trasmissione sono dati da:
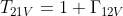
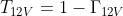
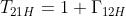
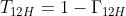
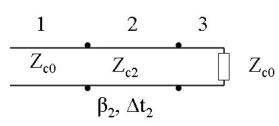
Per tener conto del fatto che la lastra intermedia ha spessore limitato, si può stabilire una
equivalenza con il problema di linee di trasmissione mostrato nella sottostante figura.
Per la polarizzazione verticale si ha:
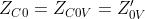
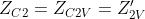
Per la polarizzazione orizzontale si ha:
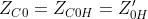
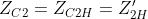
La costante di propagazione nella direzione dell’asse z sarà data da:
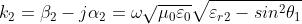
Nella generica polarizzazione il coefficiente di riflessione totale sarà dato da:
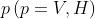
…..
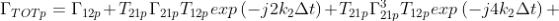
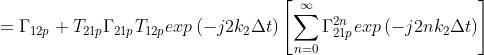
I termini della sommatoria sono quantità complesse di modulo minore di 1.
Si ha quindi una serie, per la quale vale la:
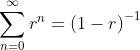
Si ottiene quindi:
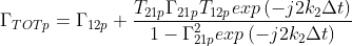
Il coefficiente di trasmissione totale sarà dato da:
+….
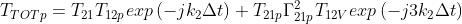

Procedendo analogamente al caso della riflessione, si ottiene
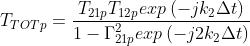
Naturalmente, sarà .
Le frazioni di potenza riflessa e trasmessa saranno date, rispettivamente, da
.
Nei casi reali il modello precedentemente descritto, basato sull’ipotesi di lastra uniforme,
va modificato per tener conto delle disomogeneità (es. strutture a mattoni con pieni e
vuoti) e della eventuale presenza di elementi metallici, di cui possono variare molto le
dimensioni e le spaziature.
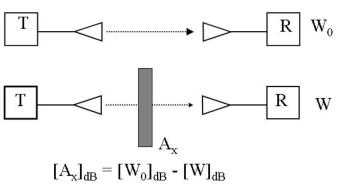
Per approfondire la conoscenza del problema, stanno avendo luogo numerose attività
sperimentali, nelle quali l’attenuazione introdotta dalle pareti è stimata per confronto tra i
coefficienti di trasmissione che si misurano tra coppie di antenne in assenza di pareti
frapposte e quelle che si misurano in presenza di esse .
Alle frequenze di 800-900 MHz, valori tipici di attenuazione sono i seguenti:
• 4-8 dB per pareti non metalliche;
• fino a circa 25 dB per pareti con elementi metallici.
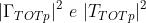
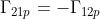


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor
Radiotecnica



