



L'ironia e l'intelligenza sono sorelle di sangue
Radiotecnica

..può sembrare che la tecnica abbia
poco valore, ma è solo l'illusione di
chi la acquisisce e la adopera,
sapendone poco o niente.....




IL CASO DELL’OSTACOLO E DELLO SPECCHIO
Il problema dell’ostacolo è trattato in forma approssimata
con il modello a lama di coltello.
Si suppone, come mostra la sottostante figura che, a distanza d1
dall’antenna trasmittente, sia presente uno schermo assorbente
disposto ortogonalmente alla congiungente tra le due antenne.
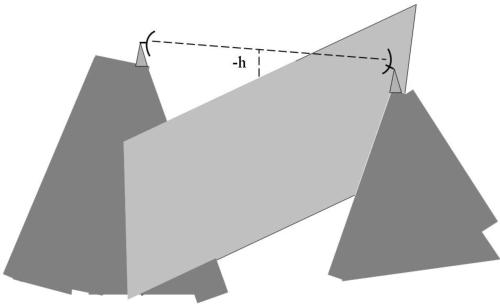
Può essere applicata la teoria descritta precedentemente, considerando un’apertura illimita-
-ta con:
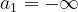
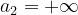
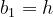
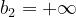
h sarà positivo se l’ostacolo si estende oltre la congiungente tra le antenne, mentre
sarà negativo se l’ostacolo non raggiunge tale congiungente.
In questo secondo caso, il valore assoluto |h| prende il nome di franco.
Per le preceenti relazioni, si ha:
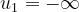
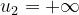
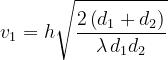
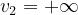
Quindi, si avrà :
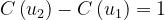
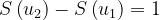
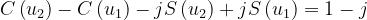
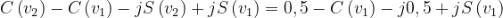
Il fattore di diffrazione, quindi, sarà:
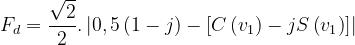
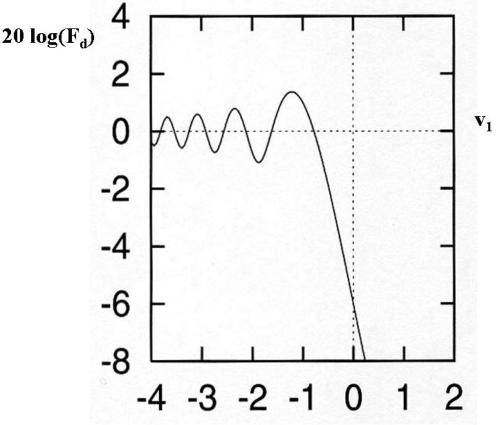
L’andamento del fattore di diffrazione (in dB) in funzione di
è riportato nella sottostante
figura.
Si nota quanto segue.
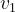
•
Per , come è ovvio in base alla definizione.
•
Per . Ciò significa che, quando l’ostacolo tocca la congiungente
tra le antenne, il campo ricevuto si riduce alla metà e la potenza ricevuta alla quarta
parte.
•
Al crescere di v1 verso valori positivi, l’ostacolo maschera sempre di più la congiungente
tra le antenne e Fd tende rapidamente a 0.
Per descrivere questa situazione, si utilizzano formule semplificate, che approssimano
bene la teoria esatta.
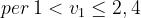
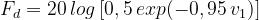
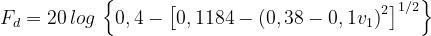
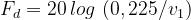
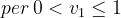
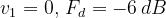
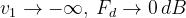
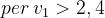
Si usa una formula approssimata anche per valori di v1 moderatamente negativi, tali
da non raggiungere il primo massimo del diagramma di cui sopra :
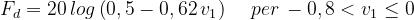
•
Per v1 < 0 c’`e un andamento caratterizzato da massimi e minimi, che trova interpre-
-tazione grafica nella spirale sopra descritta.
Dal punto di vista fisico, la spiegazione sta nelle cosiddette zone di Fresnel.
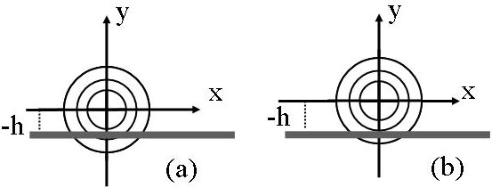
Si consideri la sottostante figura, una generica circonferenza, di raggio r’ , apparte-
nente al piano xy.
Siano r1 ed r2 le distanze che i punti della circonferenza hanno dall’antenna
trasmittente e ricevente, rispettivamente.
Il cammino elettromagnetico totale passando per i punti della circonferenza sarà
r1 + r2.
La differenza tra tale cammino e quello minimo, che si ha procedendo lungo la
congiungente rettilinea, sarà:
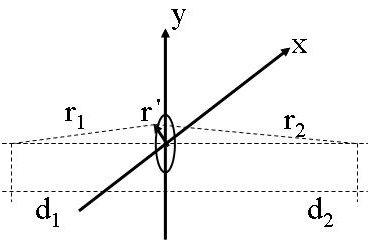
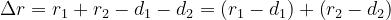
Poichè
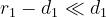
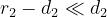
si ha:
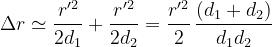
A tale differenza di cammino corrisponderà una differenza di fase data da:
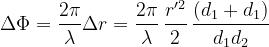
Si definisce prima zona di Fresnel il luogo dei punti per cui .
Quindi, dovrà essere:
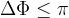
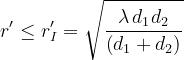
I punti appartenenti alla prima zona di Fresnel contribuiscono sostanzialmente in
fase al campo ricevuto dall’antenna ricevente.
In modo analogo, si definisce seconda zona di Fresnel il luogo dei punti per cui
Quindi, dovrà essere:
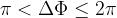
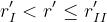
con
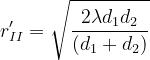
I punti appartenenti alla seconda zona di Fresnel contribuiscono sostanzialmente in
opposizione di fase al campo ricevuto dall’antenna ricevente.
Possono essere definite in modo analogo le zone di Fresnel di ordine superiore.
L’andamento della precedente figura, pertanto, può essere interpretato come segue.
Il fattore di diffrazione presenta il primo massimo quando l’ostacolo non tocca la prima
zona di Fresnel, ma maschera parzialmente la seconda (vedi la soprastante figura (a)).
Presenta, invece, il primo minimo quando l’ostacolo non tocca la seconda zona di Fresnel,
ma maschera la terza (vedi figura (b)).
Aumenti ulteriori di h verso valori negativi produrranno un alternarsi di massimi e minimi
(che, però, saranno sempre meno accentuati) a seconda che siano mascherate zone di
Fresnel di ordine pari o di ordine dispari.
Al variare di d1 e d2, le circonferenze che delimitano le zone di Fresnel descrivono
ellissoidi, detti ellissoidi di Fresnel.
Dal punto di vista applicativo, occorre distinguere tra due casi fondamentali.
Nel caso di collegamenti punto-punto fissi è opportuno progettare il collegamento in
modo che tutti gli ostacoli siano esterni al primo ellissoide di Fresnel.
Nel caso di sistemi di radiodiffusione o con mezzi mobili,possono verificarsi situazioni in
cui il primo ellissoide di Fresnel sia mascherato, o perfino si abbia .
Occorre allora calcolare il fattore di diffusione usando le relazioni già enunciate.
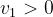
Il caso dello specchio
Sia dato uno specchio quadrato di lato a, collocato a distanza d1 dall’antenna
trasmittente, d2 dall’antenna ricevente.
Supponiamo inoltre, come avviene in pratica, che l’angolo formato dalla direzione di
incidenza e da quella di riflessione con la normale allo specchio siano piccoli.
Può essere applicata la trattazione delle precednti pagine.
Per il principio delle immagini, è come se le antenne fossero collegate da un’unica
congiungente rettilinea e a distanza d1 dalla trasmittente fosse presente uno schermo
con un’apertura quadrata, come mostra la sottostante figura, con :
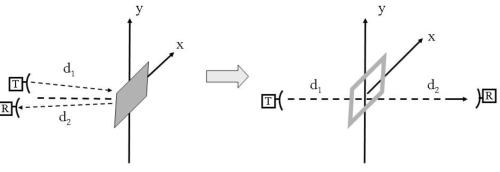
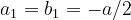
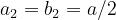
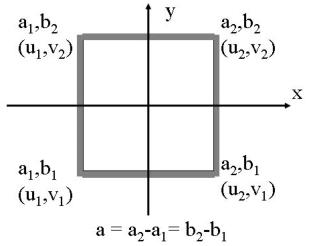
Facendo riferimento alla figura a lato, avremo:
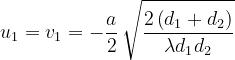
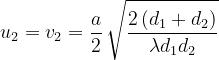
Le S(w) e C(w) sono funzioni antisimmetriche rispetto all’origine.
Dalla precedente relazione enunciata, si ottiene pertanto, per il fattore di diffrazione, la
seguente espressione:
Anche in questo caso si ha per e .
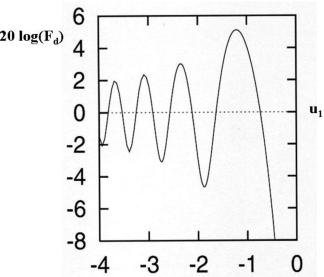
Al variare di u1, si ottiene l’andamento riportato
nella figura a lato.
Anche in questo caso si nota la presenza di
massimi e minimi, che sono più accentuati
rispetto al caso dell’ostacolo.
Si può ancora interpretare il risultato in termini
di zone di Fresnel.
Scegliendo opportunamente d1, d2 e le
dimensioni dello specchio, si può far sì che
lo specchio contenga al suo interno solo la prima
zona di Fresnel.
In questo caso la potenza ricevuta può essere
maggiore di quella che si sarebbe avuta con
due antenne in visibilità diretta.
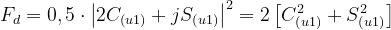
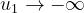
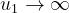
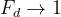


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor
Radiotecnica



