



Il software è come il sesso, è migliore quando è libero e gratuito
Radiotecnica

..può sembrare che la tecnica abbia
poco valore, ma è solo l'illusione di
chi la acquisisce e la adopera,
sapendone poco o niente.....




TEORIA DELLA DIFFRAZIONE DA APERTURA
Per analizzare il problema della diffrazione occorre ricollegarsi
alla teoria delle aperture .
Sia dato lo schema mostrato nella sottostante figura.
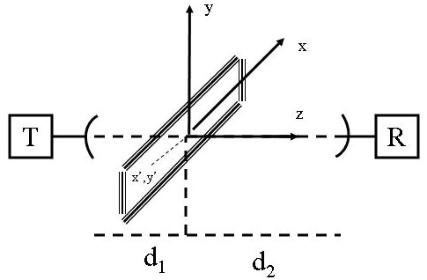
Si hanno un’antenna trasmittente (T) e un’antenna ricevente (R).
A distanza d1 dall’antenna trasmittente è presente uno schermo assorbente illimitato,
ortogonale alla congiungente tra le due antenne, e all’interno del quale è praticata una
apertura rettangolare.
Si prenda un sistema di riferimento con l’origine nel punto di intersezione tra il piano
dello schermo e la congiungente tra le due antenne, asse x orizzontale, asse y verticale e
asse z coincidente con la congiungente stessa.
Siano x’ e y’ le coordinate di un generico punto dell’apertura.
L’antenna trasmittente irradia.
Se la distanza d1 è elevata rispetto alle dimensioni dell’antenna trasmittente, sull’apertura
sarà presente un fronte d’onda sferico.
Nell’origine del sistema di riferimento, il campo incidente sarà dato da:
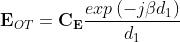
è una costante vettoriale dipendente dall’antenna e β è la costante di propagazione.
Per un generico punto del piano xy, di coordinate x’ e y’ , la distanza dall’antenna trasmit-
-tente sarà
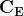
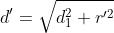
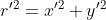
con
Supponendo si ha

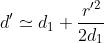
Il campo quindi sarà dato da:
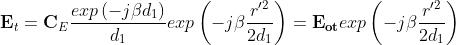
Utilizzando il teorema di equivalenza e la teoria della radiazione, è possibile dimostrare
che il campo reirradiato nel semispazio z > 0 è dato da
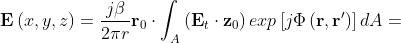
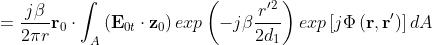
r è il vettore di posizione del punto di osservazione, r◦ `e il versore corrispondente.
A è l’area dell’apertura praticata nello schermo.
Il prodotto ( ) è la corrente magnetica equivalente sull’apertura.
Il contributo della corrente magnetica va moltiplicato per 2, per tener conto di un uguale
contributo dovuto alla corrente elettrica.
Si spiega così perchè a denominatore figura
e non
.
Se la distanza r è sufficientemente elevata, il fattore può essere approssimato
con i primi due termini dello sviluppo in serie:
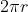
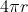
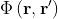

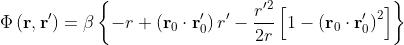
[NOTA. Nei problemi di radiazione da antenne, in generale la distanza del punto di
osservazione è molto alta rispetto alla dimensione dell’apertura, per cui si può
trascurare il terzo termine della soprastante relazione (approssimazione di campo
lontano). Nei problemi di diffrazione da ostacolo o specchio, invece, occorre tener
conto di tutti e tre i termini.]
La soprstante approssimazione prende il nome di approssimazione di Fresnel.
Usando un sistema di coordinate sferiche centrato nell’origine, si ha:
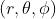

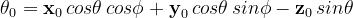
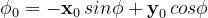
Per individuare il punto di osservazione si useranno le coordinate sferiche sopra definite.
Per semplicità, e senza limitare la generalità della trattazione, supponiamo inoltre che il
campo elettrico sia polarizzato verticalmente.
Supponiamo ancora che si abbia ampiezza costante sull’apertura.
Si ha allora:

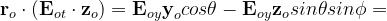
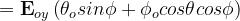
Per determinare il campo in prossimità dell’antenna ricevente teniamo conto che,
per come è stato scelto il sistema di riferimento, il punto di osservazione sarà collocato
sull’asse z, a distanza d2 dall’origine.
Poniamo quindi:

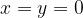
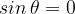
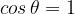
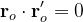
Si avrà:
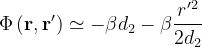
Il campo in prossimità dell’antenna ricevente sarà dato da:
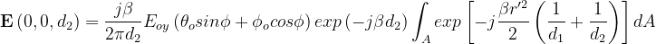
Considerando un’apertura rettangolare che si estende da x = a1 a x = a2 lungo
l’asse x, da y = b1 a y = b2 lungo l’asse y (non necessariamente centrata nell’origine),
si ha:
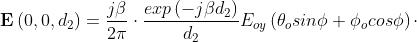
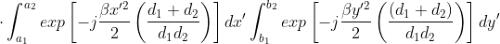
La soluzione è data dal prodotto tra due integrali di forma simile. Poniamo:
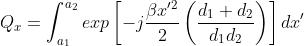
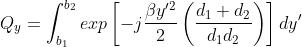
Per il calcolo del primo integrale poniamo:
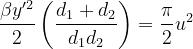
da cui
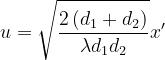
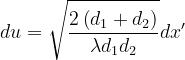
Si ha
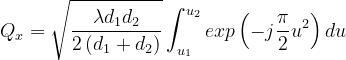
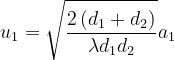
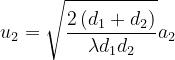
L’integrale che figura nella [1] è il cosiddetto Integrale di Fresnel complesso I(w).
Quindi:
[1]
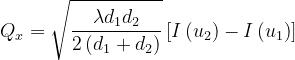
Si ha
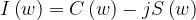
con

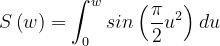
Le funzioni C(w) e S(w) sono disponibili in forma di tabelle o routines.
Si può procedere analogamente anche per Qy, ottenendo:
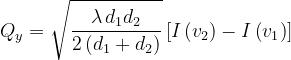
dove:
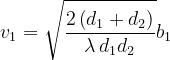
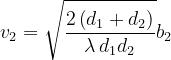
Si ricorda che:
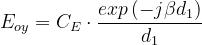
Facendo le opportune combinazioni, si ottiene:
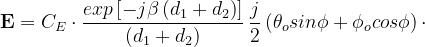

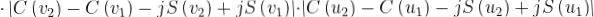
Un’utile rappresentazione grafica del risultato della soprastante equazione può essere
ottenuta riportando la S(w) in funzione della C(w), come mostrato nella sottostante figura.
Si ha la cosiddetta Spirale di Cornu.
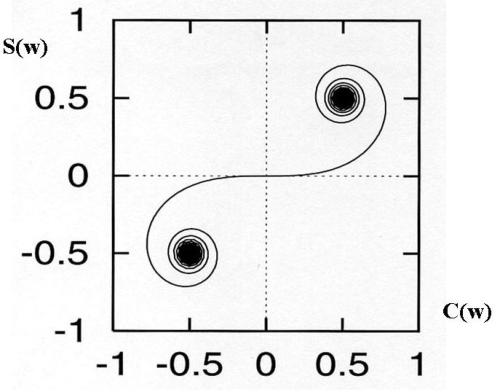
Si hanno le seguenti proprietà.
•
•
•
:
Le funzioni C(w) e S(w) raggiungono i valori limite con un andamento non monotono.
C’ è un alternarsi di massimi e minimi.
•
Il valore massimo del modulo è ottenuto per
, e vale
.
Naturalmente, il valore limite del modulo per
è 0.707.
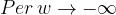
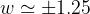
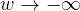

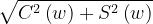


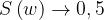

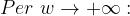
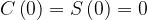
Si definisce fattore di diffrazione il rapporto tra l’ampiezza del campo ricevuto e
quella che si sarebbe avuta in assenza dello schermo con apertura.
L’ipotesi di assenza di schermo corrisponde a far estendere fino all’infinito l’apertura.
Si avrebbe, in quel caso:
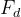
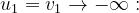
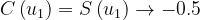
•
•
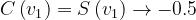

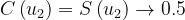
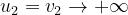
:
•
•
Tenendo conto che:
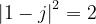
si ottiene:




Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor
Radiotecnica



