



Poni in discussione tutto. Impara qualcosa. Non rispondere niente
Radiotecnica

..può sembrare che la tecnica abbia
poco valore, ma è solo l'illusione di
chi la acquisisce e la adopera,
sapendone poco o niente.....




PROPRIETA’ DIELETTRICHE DELLA SUPERFICIE
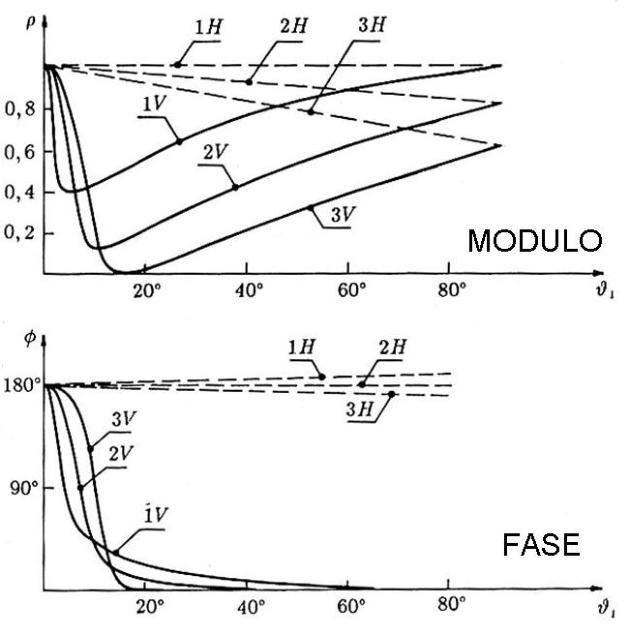
Il coefficiente di riflessione della superficie può essere
espresso con le seguenti espressioni approssimate.
Polarizzazione verticale:
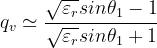
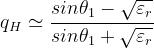
Polarizzazione orizzontale:
La sottostante figura mostra gli andamenti del modulo e della
fase per le due polarizzazioni e per i seguenti tre diversi casi:
1.
Mare f=100MHz
2.
Mare f= 3 GHz
3.
Terreno mediamente umido, 100 MHz < f < 3 GHz
Si nota quanto segue.
•
In polarizzazione orizzontale il coefficiente di riflessione si discosta poco dal valore
-1, anche per θ1 molto maggiore di 0°.
•
In polarizzazione verticale il coefficiente di riflessione presenta un forte abbassamento
in modulo, tipicamente per piccoli angoli, a cui corrisponde una discontinuità di 180°
nella fase.
Il valore di θ1 per cui si ottiene il minimo è detto angolo di Brewster.
Nel caso del terreno, poichè la parte reale della costante dielettrica è dominante, si hanno
valori quasi nulli.
Nel caso del mare, invece, si ha una apprezzabile parte immaginaria, specialmente alle
frequenze più basse.
Pertanto, si avrà un minimo, ma con valori sensibilmente maggiori di zero.
Poichè nei radiocollegamenti i valori di θ1 sono in genere piccoli, quindi prossimi
all’angolo di Brewster, in polarizzazione verticale il modulo del coefficiente di riflessione
potrà essere sensibilmente minore di 1.
Effetti della rugosità della superficie
Nella realtà il terreno non è mai perfettamente liscio, ma presenta rugosità più o
meno accentuate.
Esistono, poi, situazioni particolari (es. rilievi, vegetazione, zone edificate) nelle quali
le irregolarità sono tali da eliminare completamente il fenomeno della riflessione speculare.
Analogamente, la superficie marina presenta irregolarità più o meno elevate a seconda
del moto ondoso.
Quando è presente rugosità di piccola scala, la potenza riflessa dalla superficie è data
dalla sovrapposizione di due componenti:
•
una componente è ancora riflessa specularmente, ma le rugosità ne riducono
l’entità (componente coerente);
•
un’altra componente è diffusa dalla rugosità in modo irregolare in tutte le direzioni
(componente incoerente).
Per la componente coerente, risulta applicabile la seguente espressione:
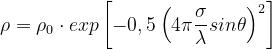
è il modulo del coefficiente di riflessione,
è quello che si sarebbe avuto con una superficie liscia delle stesse proprietà dielettriche,
σ è la deviazione standard dei discostamenti dalla superficie media
θ è l’angolo di radenza (rispetto al piano orizzontale).
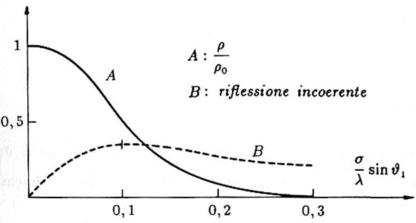
Come si ha spesso nei problemi di elettromagnetismo, la variabile σ è scalata rispetto a λ.
L’andamento del rapporto ρ/ρ◦ è riportato nella sottostante figura, insieme all’andamento
corrispondente della frazione di potenza che è riflessa in modo incoerente.
Dal punto di vista applicativo, la presenza di rugosità determina, pertanto, due
conseguenze.
•
La riflessione speculare diminuisce.
•
Si manifesta una componente non speculare, che può generarsi lungo tutto il
collegamento.
Può dare effetti rilevanti quando si genera in prossimità dell’antenna ricevente.
Effetti della rotondità terrestre
La sottostante figura mostra il processo di riflessione, tenendo in conto la rotondità
terrestre.
Supponendo che la potenza irradiata dall’antenna trasmittente sia contenuta in un cono
di apertura ∆θ1, dopo riflessione da una superficie sferica la potenza sarà distribuita in
un cono di apertura ∆θ2 > ∆θ1, per cui sarà meno concentrata e più dispersa.
Essendo la densità di potenza minore, sarà minore la potenza captata dall’antenna 2.
Di questo effetto si può tener conto modificando la precedente espressione, in modo
da introdurre un fattore di divergenza D < 1.
Si avrà quindi

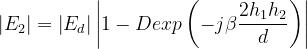
Effetti atmosferici
Per ragioni che saranno discusse successivamente, l’atmosfera rende curvilinei i
percorsi elettromagnetici diretto e riflesso.
Pertanto, anche la differenza r1 +r2 −r sarà alterata rispetto al caso ideale trattato
in precedenza.
Tale alterazione dipenderà dalle condizioni atmosferiche, per cui sarà variabile nel
tempo.
Considerazioni conclusive
Si possono trarre le seguenti considerazioni conclusive.
•
Se sono valide tutte le ipotesi semplificative, il modulo del campo ricevuto può
avere un’ampiezza variabile tra 0 e il doppio di quella che si avrebbe in assenza di
riflessioni.
La corrispondente potenza varierà tra 0 e il quadruplo.
•
Gli effetti delle proprietà dielettriche, della rugisità e della rotondità terrestre
riducono l’ampiezza del campo riflesso.
Nella realtà, quindi, si avranno comunque possibili variazioni dell’ampiezza del campo
ricevuto rispetto a |Ed|, ma di entità limitata.
•
Gli effetti atmosferici rendono l’ampiezza del campo ricevuto variabile nel tempo, in
modo irregolare.
Diffrazione dalla rotondità terrestre
Date due antenne disposte ad altezze h1 e h2, del tipo di quelle già considerate nel
paragrafo precedente, la rotondità terrestre pone un limite massimo alla distanza di
visibilità ottica.
Con riferimento alla sottostante figura, definendo con RT il raggio terrestre, tale limite
può essere calcolato dalle:
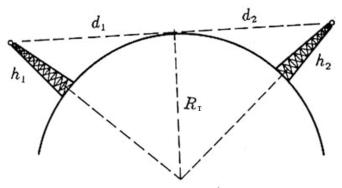
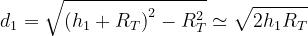
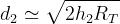
Si ha quindi:
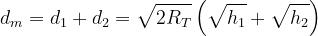
è la distanza massima, approssimabile a
quella che si ha procedendo lungo l’arco.
Se d > , il passaggio ad una situazione di totale isolamento tra le due antenne sarà
graduale.
A causa della diffrazione dovuta alle correnti indotte sulla superficie terrestre, infatti,
sarà ancora possibile ricevere apprezzabile potenza anche aldilà della visibilità geome-
-trica. La teoria è complessa.
Tuttavia, è possibile approssimare i risultati con forme algebriche semplici.
Si definiscono i parametri normalizzati X, Z1 e Z2 nel seguente modo.
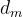
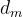
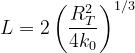
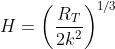
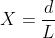
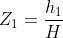
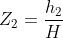
Definendo Fd il fattore di diffrazione, cio`e il rapporto tra il campo ricevuto e quello
che si sarebbe ricevuto nel vuoto, si ha:
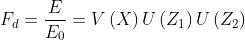
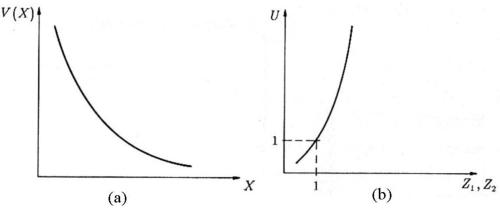
Gli andamenti delle funzioni sono mostrati nelle sottostanti figure
[a] e [b].
La V (X) è una funzione decrescente, approssimabile come:
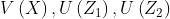
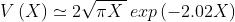
Esprime quanto si perde aumentando la distanza tra le antenne.
La invece è crescente, ed esprime quanto si recupera aumentando l’altezza
delle antenne.
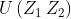
Diffrazione da ostacoli e specchi
Alcuni problemi propagativi sono riconducibili alla teoria della diffrazione da aperture.
Due esempi classici sono quello dell’ostacolo e quello dello specchio.
Il problema dell’ostacolo si pone quando, lungo la tratta che congiunge due antenne,
sono presenti rilievi o edifici tali da alterare, più o meno estesamente, le proprietà
dell’onda rispetto a quelle che si avrebbero nel vuoto.
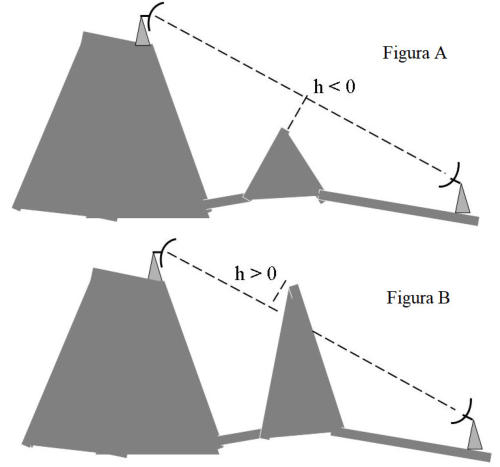
Nel caso della figura [A] l’ostacolo è al di sotto della congiungente tra le due antenne,
per cui introduce perturbazioni limitate, anche se non trascurabili.
Nel caso della figura [B] l’ostacolo è al di sopra della congiungente stessa, per cui
produce attenuazione molto forte, anche se, proprio per la diffrazione, la potenza che
raggiunge il terminale ricevente può essere ancora apprezzabile.
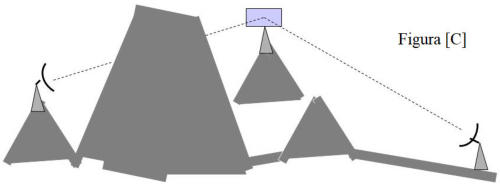
In molti collegamenti che operano in presenza di rilievi, proprio per evitare il problema
degli ostacoli, si usano ripetitori passivi, detti specchi, aventi forma piana e buona
conducibilità, che reirradiano verso l’antenna ricevente la potenza proveniente
dall’antenna trasmittente (figura [C]).
Sia per il problema delle figure [A] e [B] che per quello della figura [C], si ricorre alla
teoria della diffrazione da apertura.
Nel primo caso si assume che il piano ortogonale alla congiungente tra le antenne e
passante per l’ostacolo agisca come uno schermo assorbente, avente al suo interno
un’apertura che è illimitata nella direzione orizzontale e, verso l’alto, nella direzione
verticale.
Nel secondo caso l’apertura è limitata e coincide con lo specchio stesso.
Le relative teorie sono illustrate nel seguito.


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor
Radiotecnica



