PROPAGAZIONE PER ONDA SUPERFICIALE

Le frequenze fino a 30 MHz sono usate per sistemi di radiodiffusione, caratterizzati da antenne a traliccio di notevoli dimensioni e, in genere, alimentate a terra in modo unipolare, come mostrata in figura:

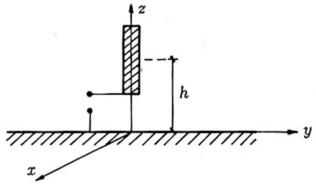
Una struttura di questo tipo, essendo piccola rispetto alla lunghezza d’onda (1 MHz corrisponde a 300 m), può essere approssimata da un dipolo elementare. Pertanto, se h è la semi-altezza dell’antenna, questa può essere considerata come sede di correnti elettriche impresse aventi la seguente espressione:

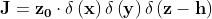
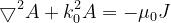
Per il potenziale vettore magnetico A valgono le seguenti equazioni

per z>0

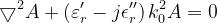
per z<0

dove è la costante di propagazione nel vuoto.

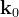
Si impongono poi le condizioni di continuità dei campi elettrico e magnetico tangenziali per z = 0. La trattazione matematica del problema, che risale a prima del 1940, è stata oggetto di discussioni e approfondimenti. E’ stato dimostrato che, a distanze elevate dalla sorgente, esiste una soluzione delle sopracitate formule, associata a propagazione lungo il piano orizzontale, mentre c’ è forte attenuazione sul piano verticale. Si ha cioè la cosiddetta onda superficiale. L’interpretazione fisica è la seguente. Le correnti che scorrono sull’antenna e sulla zona di terreno circostante irradiano. Il campo irradiato induce a sua volta correnti nelle zone circostanti, e così via. Al crescere della distanza si ha perdita di potenza dovuta a dispersione nella direzione radiale e assorbimento del terreno. Ciononostante, il livello ricevuto può essere apprezzabile fino a centinaia di chilometri. Il risultato della trattazione viene espresso in una forma del tipo:

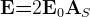
Dove è il campo elettrico ricevuto, è il campo elettrico che si sarebbe avuto per propagazione nel vuoto, ed è un fattore dipendente dalla distanza, dalla freque- -nza e dalla costante dielettrica del terreno. Per esprimere in funzione di queste variabili vengono usate formule polinomiali che sono approssimazioni della soluzione teorica del problema.

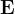
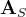
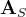
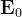
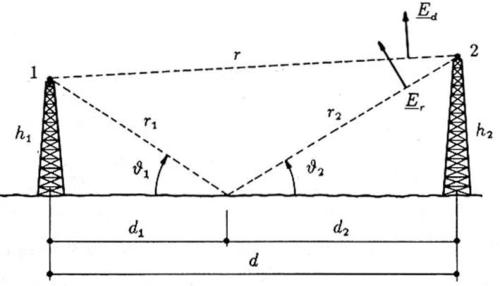
Riflessione dal terreno Si consideri (come mostrato nella sottostante figura) un collegamento, tipicamente ponte-radio, caratterizzato da una coppia di antenne direttive, poste rispetto al terreno ad altezze h1 e h2, grandi rispetto alle dimensioni delle antenne stesse. Sia d la distanza tra di esse.

A differenza dei sistemi di radiodiffusione, che operano su tutta l’area circostante, in questo caso ciascuna delle due antenne è progettata e posizionata in modo tale da concentrare il massimo di potenza irradiata nella direzione dell’altra. Il terreno, che nel caso della propagazione guidata interveniva lungo tutto il collegamento, fin dalla costruzione stessa delle correnti, in questo caso interviene solo con un effetto localizzato. Ciò è conseguenza delle frequenze relativamente elevate (tipicamente maggiori di 1 GHz) usate in questi sistemi. A queste frequenze, il meccanismo di propagazione guidata è fortemente attenuato. Per caratterizzare teoricamente il problema, si faccia riferimento alla soprastante figura. Si tenga conto che non è in scala, in quanto h1 e h2 sono di qualche metro, mentre d è almeno qualche decina di chilometri. Le due antenne sono in genere rice-trasmittenti ma, per semplicità, supponiamo che sia trasmittente la 1 e ricevente la 2 (il problema è reciproco). Partiamo dalle seguenti ipotesi semplificative.

1. L’effetto del terreno è riconducibile ad una riflessione localizzata in una zona molto piccola rispetto a d. Di conseguenza si hanno due percorsi: uno diretto, di lunghezza r ed uno riflesso di lunghezza r1 + r2, indipendenti tra loro. 2. Data l’elevata distanza i campi associati ai due cammini, che chiameremo Ed ed Er, in prossimità dell’antenna ricevente sono rappresentabili come onde piane, e tra loro paralleli. 3. Il terreno è liscio. Ciò comporta che la riflessione è speculare e ha luogo nella zona in cui: θ1 e θ2 sono molto piccoli. 4. Si suppone di avere riflessione totale. Il coefficiente di riflessione sar`a allora: 5. Si trascura la rotondità terrestre. 6. Si trascurano gli effetti atmosferici. Le prime due ipotesi sono ragionevolmente valide, e saranno mantenute in tutta la trattazione. Per le altre quattro, invece, possono aversi situazioni reali in cui non sono verificate, anche sensibilmente. Pertanto, si partirà dal caso ideale in cui tutte e sei le ipotesi sono verificate, poi si considereranno le modifiche da introdurre per il mancato soddisfacimento, in diversa misura, delle ultime quattro.

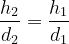
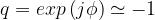
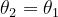
Caso ideale Il campo totale in prossimità dell’antenna 2 (E2), sarà dato dalla somma del contributo dell’onda diretta (Ed) e di quello dell’onda riflessa (Er): dove:

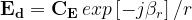
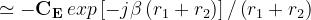
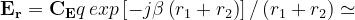
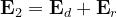
è una costante vettoriale dipendente dall’antenna trasmittente. Si suppone che abbia lo stesso valore nei due casi, trascurando l’effetto della piccola variazione angolare θ1. β è la costante di propagazione. Ai fini dell’ampiezza si può supporre:

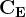
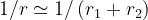
Ai fini della fase, invece, poichè la lunghezza d’onda λ è di qualche cm, anche piccoli valori della differenza tra (r1+r2) ed r vanno tenuti in conto, in quanto possono corrispondere a molte periodicità. Si ha, quindi:

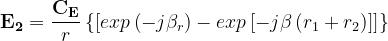
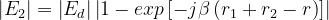
Si ha inoltre, tenendo conto che :

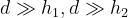
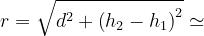
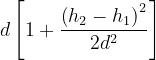
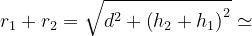
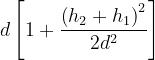
Ne consegue :

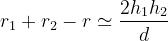
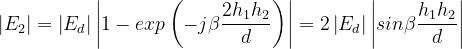
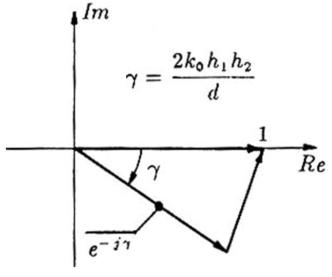
Come evidenziato in figura:

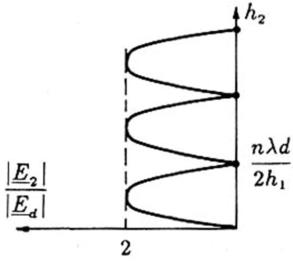
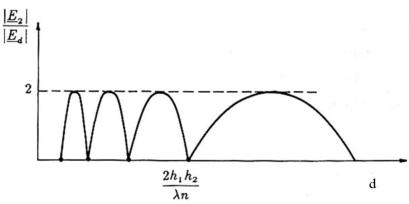
Se si fa variare h2 mantenendo costanti gli altri parametri si ottiene l’andamento della figura a destra. mentre se si fa variare d mantenendo costanti gli altri parametri si ottiene l’andamento della sot- -tostante figura. Il campo ricevuto oscilla tra massimi pari a 2|Ed| e nulli. Tali oscillazioni sono conseguenti alle ipotesi di partenza, per le quali |Er| = |Ed|, e cor- -rispondono alle situazioni di interferenza costruttiva (massimi) e distruttiva (nulli) tra i due campi. Si noti come i nulli corrispondenti a variazioni di h2 sono equispaziati, mentre quelli corrispondenti a variazioni di d sono a spaziatura crescente. Considereremo, nel seguito, le conseguenze delle diversità dei terreni reali rispetto alle ultime quattro ipotesi semplificative.