



Adesso sono più conosciuto: faccio cilecca con donne più belle.
LE DERIVATE : MOTIVAZIONI

… studiare, studiare ed ancora
studiare, è il solo modo di capire
quanto possa essere grande
la propria ignoranza!

Ancora sulla derivata di una funzione : le motivazioni
Abbiamo gia visto come il concetto di limite consente di gestire il
problema della valutazione di una funzione.
Non ci consente però di stimare la monotonia di una funzione
(crescente o decrescente?)
e di valutarne la velocità
di variazione.
Ad esempio per le tre
funzioni riportate in figura
a lato si ha che il limite
per x tendente a 1 è uguale
a 1.
La loro monotonia è
ovviamente differente.
In particolare una di esse è decrescente, le altre due sono crescenti. Queste ultime,
inoltre, sembrano mostrare una differente "velocità di crescita".
Ci occorre dunque un
"indice di variabilità" che consenta di:
•
Stabilire la monotonia di una funzione (puntuale).
•
Quantificare la velocità di variazione (se la funzione è crescente "intorno" ai punti
a e b del suo dominio, è possibile stabilire in quale punto la crescita è più veloce?
Fra due funzioni, entrambe crescenti in un punto, è possibile quale delle due
cresce più velocemente?)
Notiamo che per la funzione
sappiamo
rispondere alle due domande
precedenti: la monotonia
dipende dal coefficiente
angolare m (se positivo, la
funzione è crescente, se
negativo decrescente) e, fra
due rette aventi coefficiente
angolare positivo, quella con
coefficiente angolare
maggiore ha pendenza
maggiore.
Vediamo dal grafico
interattivo a fianco, che il
rapporto incrementale
coincide con il coefficiente
angolare della retta per A e
B (secante il grafico nei punti
.
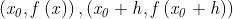

Abbiamo due tipi di rapporto
incrementale :
Rapporto incrementale positivo
Dove la funzione cresce passando da a
Rapporto incrementale negativo
Dove la funzione decresce passando da a
Il rapporto incrementale positivo garantisce che la funzione decresce passando da
a ma non che decresce fra e .
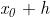

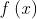
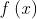

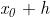

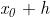

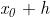
Consideriamo una funzione in un intervallo [a,b] e sia
un fissato punto interno all’intervallo .
Adesso passiamo dal punto ad un altro punto interno
all’intervallo

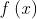



Ciò facendo si fornisce cioè un certo incremento, che detto h,
al valore tale da trovarsi ancora nell’intervallo .


Osservazione :
•
se ci si sposta alla destra di
•
se ci si sposta alla sinistra di
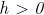
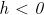


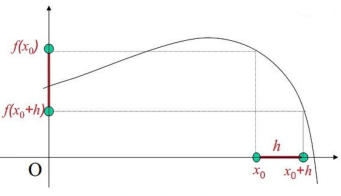
Il passaggio da ad lungo l’asse delle
ascisse viene detto incremento della variabile
x e coincide col valore h
Le immagini f dei punti ed sono
rispettivamente ed .
La differenza f( tra i valori che
la funzione assume passando da ad prende il nome di

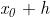

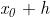




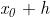
incremento della funzione f
Il valore dell'incremento della funzione può essere positivo, negativo o nullo.

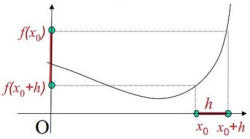
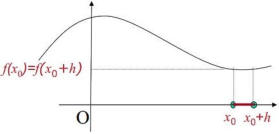

Detto valore di incremento della funzione f nel passaggio
da a è
•
negativo se decresce passando da ad
•
positivo se cresce passando da ad
•
nullo se rimane costante passando da ad
.
L'incremento della variabile x viene indicato con il simbolo
"
"
L'incremento della funzione f viene indicato con il simbolo
"
"
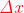

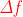

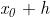
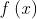


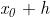
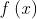
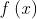

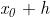

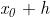
Il rapporto tra l'incremento della variabile x nel passaggio da ad e
l’incremento della funzione f, viene denominato rapporto incrementale della funzione
f al passaggio da ad , ovvero :

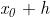


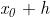
Il rapporto incrementale, in altri termini, esprime la " variabilità di f " relativamente ad
un certo intervallo.
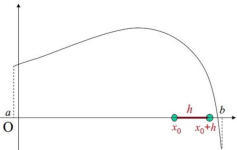
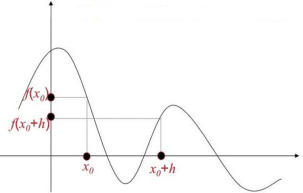
Dal grafico a lato, si esemplifica che il rapporto
incrementale della funzione considerata nel
passaggio da ad è negativo.
Quindi la funzione considerata sicuramente
decresce nel passaggio da a ma non
decresce in tutto l'intervallo , dove
infatti è prima decrescente e poi crescente.
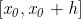

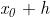

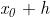
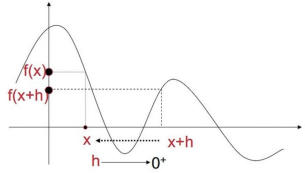
Una informazione puntuale in un punto circa la
monotonia, richiede che si consideri un
" intervallo [ x0, x0+h ] molto piccolo ".
Questo si ottiene quando il punto si avvicina
al punto e cioè quando l'incremento h diventa
sempre più piccolo.

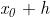

Prendiamo in considerazione una funzione in un intervallo e sia un
fissato punto interno all'intervallo .
Si definisce derivata della funzione f(x) nel punto x0 il limite, se esiste ed è finito,
del rapporto incrementale di f nel passaggio da x ad x+h, al tendere a zero
dell'incremento h della variabile indipendente x.





Questa è la derivata della funzione f nel punto x.
Questa è la derivata della funzione f nel punto x.





Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor



