



Ma quando un vegetariano muore si reincarna o si 'reinverdura'?.
LE DERIVATE

… studiare, studiare ed ancora
studiare, è il solo modo di capire
quanto possa essere grande
la propria ignoranza!


LE DERIVATE
Le derivate di una funzione sono indispensabili nei più disparati
campi dell'analisi e della vita corrente: le derivate servono, ad
esempio, per poter disegnare i grafici delle funzioni, velocità
parziali, differenze correlate, definire una tangente ad una curva,
trovare la velocità istantanea di un punto, ecc. .
Qui troverete dalle definizioni, ai teoremi di calcolo, fino ad
arrivare ai risultati teorici sulle derivate (che hanno millemila
applicazioni pratiche, ovvero servono come il pane in moltissime
applicazioni....)
Consideriamo una funzione di variabile reale (x) a valori reali (y).
In questa lezione introduciamo la nozione di rapporto incrementale di una funzione in
un punto del suo dominio. Come al solito, è solamente un nome (comodo) per
indicare un generico punto.
Definiamo il rapporto incrementale di in nel modo seguente: innanzitutto
prendiamo una lunghezza h sull'intervallo delle ascisse, e consideriamo







dove := indica che l'uguaglianza è una definizione. Il precedente rapporto consiste
nella divisione tra la differenza delle ordinate , , ossia le ordinate
corrispondenti alle ascisse e mediante f, e la differenza delle relative
ascisse e , che è evidentemente h.



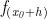


Il rapporto che indicato con : si chiama rapporto incrementale, e il nome si giustifica
per il fatto che è un rapporto di differenze calcolate a partire da un incremento: h,
per l'appunto. Δ, ovvero la lettera greca Delta, si usa solitamente in Matematica e in Fisica
per indicare una variazione o differenza, il che giustifica la notazione .
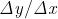
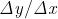
SIGNIFICATO GEOMETRICO DEL RAPPORTO INCREMENTALE
Definito ed osservato il significato di rapporto incrementale, penso che si sia capito come
si indica e perchè si indica così. Non abbiamo però la più pallida idea di che cosa significhi
dal punto di vista pratico (leggi "geometrico") né del perché lo abbiamo voluto definire.
La seconda domanda non deve, né può, trovare una risposta qui ed ora. Ricorda la regola
più importante dello studio della Matematica di base. Prima capisci come, poi capirai perché.
Non ha senso sperare di capire come e perché simultaneamente, certe domande trovano
risposta sulla strada e non all'inizio!
Per quel che riguarda l'interpretazione geometrica del
rapporto incrementale, consideriamo una funzione come
quella in figura a destra.
Non ne conosciamo la forma analitica, ossia l'espressione
, ma adesso non ce ne importa un granchè.
Ora prendiamo un punto x0 a caso e una distanza h arbitraria,
e seguiamo passo passo la definizione
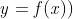
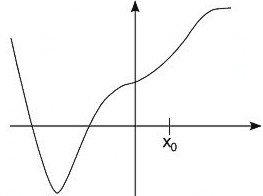
•
x0 è il punto di partenza, h una distanza sull'asse
delle ascisse
•
guardiamo l'ascissa x0+h
•
guardiamo le ordinate corrispondenti a x0 ed x0+h
mediante f
•
consideriamo e
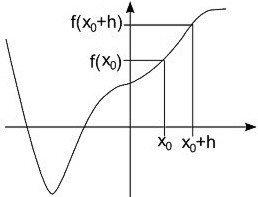
Cosa sono ?


Esattamente le lunghezze dei due cateti del triangolo
rettangolo nella figura alla tua destra.
Ecco spiegato che cos'è il rapporto incrementale di
una funzione in un punto:
la divisione tra due lunghezze.
Adesso siamo pronti a definire la derivata di una funzione....


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor



