Ci sono adolescenze che si innescano a novanta anni.

LIMITE INFINITO

… studiare, studiare ed ancora studiare, è il solo modo di capire quanto possa essere grande la propria ignoranza!

Definizione Si scrive se, per ogni intorno (e. ) del limite , esiste un intorno di c tale che, per ogni si ha anche Nella forma compatta, se :

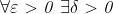
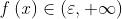
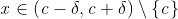
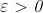
Stesse considerazioni di prima sulle differenze tra la prima definizione e la forma compatta: può essere qualunque, perchè ha il significato di estremo dell’intorno di , mentre δ torna ad avere il significato di raggio di un intorno e quindi torna ad essere positivo. Nella forma compatta, per semplicità nelle verifiche, è meglio dire . Le due forme sono infatti equivalenti. Ed ecco la definizione compatta nel caso del limite da destra e da sinistra. se :

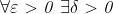
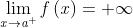
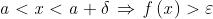
(che è rappresentato nella figura alla tua destra) ed anche se : Poi abbiamo il caso del limite Definizione. Si scrive

se per ogni intorno del limite esiste un intorno di c tale che, per ogni si ha che . Nella forma compatta se : Osservazione Si noti che qui, nella forma compatta, ho riportato e ho cambiato la disuguaglianza sulle in ( ricordati l’analogia di tutto questo con quanto fatto nel caso di limite finito all’infinito). Osservazione La solita nota operativa: per una verifica di limite nel caso di limite infinito al finito, ad esempio con limite , basta provare che per ogni l’insieme delle soluzioni della disuguaglianza , con , contiene un intorno del punto c (c come sempre escluso). Ovviamente, nel caso di limite , la disequazione da cui partire sarà

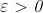
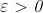
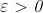
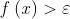
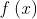
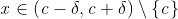
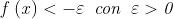
Limite infinito all' infinito Si parla di limite infinito all’infinito quando la variabile tende a e il limite è . . Dei quattro casi, vediamone però uno solo. Dei quattro casi possibili ne vediamo solo uno, lasciando al lettore il compito di scrivere la definizione di limite negli altri casi. Definizione Si scrive se per ogni intorno del limite , esiste un intorno di , tale che per si ha anche Osservazione Qui nè ε nè δ hanno restrizioni di segno, dato che sono entrambi estremi di un intorno illimitato. Nella forma compatta, come fatto prima, possiamo però chiedere che siano entrambi positivi e scrivere : In una verifica concreta basterà provare che, fissato un qualunque , l’insieme delle soluzioni della disequazione contiene un intorno di .

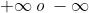
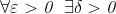
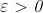
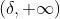
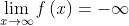
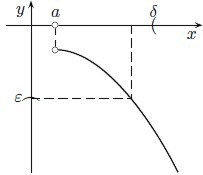
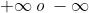
Limite infinito al finito Si parla di limite infinito al finito quando la variabile tende ad un numero reale e il limite è +∞ o -∞. Anche qui c’è ovviamente la possibilità di un limite solo da destra o solo da sinistra. Ecco la definizione nel caso del limite bilatero.

Lorem Ipsum Dolor

Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.

Add your one line caption using the Image tab of the Web Properties dialog

Made with Xara

Home