



Qualità significa fare le cose bene quando nessuno ti sta guardando.
LIMITE SINISTRO E BILATERO

… studiare, studiare ed ancora
studiare, è il solo modo di capire
quanto possa essere grande
la propria ignoranza!






Limite per x 6b- (limite sinistro)
Consideriamo sempre ,
con intervallo limitato di
Definizione : Si scrive con
se per ogni intorno del
limite l, esiste un intorno sinistro ,
tale che per ogni si ha che
Osservazione : Anche in questo caso non si chiede nulla su .






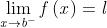
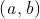
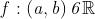
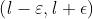
Analogamente a quanto fatto prima, la cosa si può esprimere scrivendo che
:
Osservazione (di carattere operativo) : Per provare che è vera una certa scrittura di
limite da sinistra basta provare che per ogni ε > 0 l'insieme delle soluzioni di
disequazione contiene un insieme del tipo per qualche
,
cioè un intorno sinistro di .
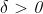




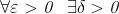
Limite per x 6c (limite bilatero)
Sia un intervallo e sia . Sia poi f : (a, b) \ {c} 6 . Tengo a ricordarti che
la scrittura indica l’intervallo privato del punto c. Quindi si considera
una funzione che è definita in , e cioè può non essere definita nel punto c..
Definizione : Si scrive
se,
per ogni intorno del limite l, esiste un
intorno di c tale che per ogni
Osservazione : Si osservi che qui, analogamente a quanto
fatto prima con i limiti da destra e da sinistra, non si chiede
nulla su , e quindi si considera l’intorno
privato del punto c. La definizione in questo caso si può dare
in forma compatta scrivendo che
Di solito il limite bilatero si chiama semplicemente limite. Quindi, dicendo limite, si allude al
limite bilatero.

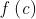
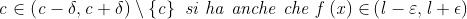

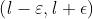

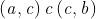
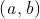
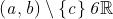
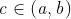
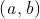

Osservazione Anche in questo caso la nota di carattere operativo. Per provare che è
vera una certa scrittura di limite bilatero basta provare che per ogni
l’insieme
delle soluzioni della disequazione contiene un insieme del tipo
per qualche
, cioè un intorno di c (con c escluso).
Osservazione Per provare invece la falsità di una certa scrittura di limite basta
trovare un particolare valore di ε per cui la condizione della definizione risulta falsa.

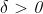


La seguente scrittura è vera :
Infatti, fissato un qualunque intorno del limite 0, osserviamo che il valore della
funzione appartiene a tale intorno se e solo se , cioè se e solo se
. Le soluzioni costituiscono proprio un intorno del punto 1, l’intorno
.
Esempio Proviamo ora con la definizione che invece non è vera la scrittura
Fissato un intorno del limite 1, consideriamo la disuguaglianza ,
cioè . Le soluzioni della disequazione sono date dall’intervallo .
Evidentemente tale insieme non contiene sempre un intorno di 1:
ad esempio, per , esso è fatto di punti esterni ad un intorno di 1. La scrittura di
limite quindi è falsa.
Esempio Proviamo che
Fissato un qualunque
che definisce un intorno del limite 1, consideriamo
la disuguaglianza , che equivale a , che equivale a sua volta
a . Si tratta di un intervallo che contiene certamente un intorno di e, dato
che
, mentre .


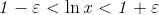





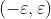



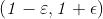



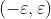
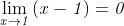


Esempio Proviamo che
Fissato un qualunque intorno del limite 0, il valore della funzione
appartiene a tale intorno se e solo se , cio`e se e solo se . Se
(ricordare che il limite `e per
), questa equivale a .
Ora, se
(e quindi
), si ottiene , che è un numero negativo.
Pertanto tutte le x positive soddisfano la disequazione ed è determinato un intorno
destro di 0.
Se invece (e quindi ), si ottiene , che è un numero
positivo. Pertanto soddisfano la disequazione tutte le x dell’intervallo , che
è ancora un intorno destro di 0.
Se infine
la disuguaglianza diventa , cioè
, insieme che contiene
un intorno destro di 0.
Osservazione Ribadisco che, dicendo “limite”, senza precisare se limite destro o
limite sinistro, si intende limite da destra e da sinistra.
Si potrebbe dimostrare rigorosamente, ma è abbastanza facile intuirlo, che il limite
esiste se e solo se esistono e sono uguali il limite destro e il limite sinistro. Può
essere comodo talvolta calcolare il limite calcolando separatamente il limite destro e
il limite sinistro.





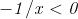
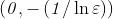


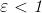



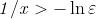


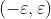
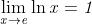


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor



