



Per riacquistare la giovinezza basta solo ripeterne le follie.
Definizione di Logaritmo

… studiare, studiare ed ancora
studiare, è il solo modo di capire
quanto possa essere grande
la propria ignoranza!





Da un punto di vista didattico il logaritmo può essere presentato in
due modi differenti:
Dopo avere dimostrato, o comunque enunciato, il seguente teorema:
Teorema: Se a è positivo e diverso da 1 e b è positivo, esiste ed
è unica la soluzione dell’equazione:
.
Si definisce il logaritmo come soluzione dell’equazione precedente
che viene indicata con l’espressione :
che si legge : Logaritmo di b in base a.

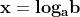
In alternativa, si definisce il logaritmo come inversa della funzione esponenziale.
Infatti, a partire dalla funzione esponenziale si fa’ osservare che essa e’
invertibile: decrescente se ; crescente se
.
E quindi si può considerare la funzione inversa: dato un valore y, x dovra’ essere
l’esponente da dare alla base per ottenere y.
In entrambi i casi si giunge alla seguente definizione:
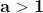

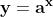
Si dice logaritmo in base a di un numero b l’esponente c
che si deve dare ad a per avere b: dove a
e` detta base del logaritmo e b argomento.

a) per a=10 si ha il sistema dei logaritmi decimali (volgari o di Briggs);
b) per a=e ≈ 2,71828 si ha il sistema dei logaritmi naturali o neperiani
I logaritmi godono di alcune proprietà. Enunciamole.
1.
Il logaritmo di un prodotto di fattori positivi è uguale alla somma dei logaritmi dei
singoli fattori ; cioè:
2.
Il logaritmo di un quoziente di due numeri positivi è uguale alla differenza tra il
logaritmo del dividendo ed il logaritmo del divisore:
3.
Il logaritmo della potenza di un numero positivo, ad esponente reale qualunque, è
uguale al prodotto dell'esponente per il logaritmo della base della potenza :
4.
lIl logaritmo in base a di un numero b diverso da 1, è uguale al reciproco del
logaritmo in base b del numero a :
5.
Il logaritmo in base a di un numero N è uguale al prodotto tra il logaritmo dello stesso
numero N in un'altra base b ed il reciproco del logaritmo di a in base b :
oppure
6.
7.
8.

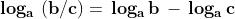

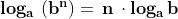




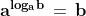


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor



