



Gioventù oziosa, schiava di tutto; coll'essere troppo sensibile ho sprecato la mia vita.
I Logaritmi

… studiare, studiare ed ancora
studiare, è il solo modo di capire
quanto possa essere grande
la propria ignoranza!





La Storia
I Logaritmi fanno la loro prima apparizione durante la Rivoluzione
scientifica: le enormi scoperte nel campo dell’astronomia (Keplero
per esempio ne fece grande uso) e della navigazione necessitavano
di un robusto apparato matematico, ma soprattutto di un operatore
in grado di rappresentare numeri molto grandi o molto piccoli.
Micael STIFEL (Esslingen, 1487 - Jena,1567, Germania) può essere
considerato il pre-inventore dei logaritmi ; nella sua opera
“Aritmetica Integra” (1544) per la prima volta comparì il calcolo di
potenze con esponenti razionali non interi e realizzò uno schema
(sotto riportato ), che costituì la prima rudimentale tavola dei
logaritmi (in base 2).
Logaritmi :
0
1
2
3
4
5
Numeri :
1
2
4
8
16
64
L'idea che sta nella base, è il confronto tra i termini della progressione geometrica di
ragione r (base del logaritmo): 1, r, r2, r3, .... e i termini della corrispondente
progressione aritmetica formata dagli esponenti
Dal punto di vista applicativo uno schema di questo tipo si può interpretare come la
corrispondenza intercorrente nella crescita di una cellula, o di una popolazione alla
quale all’istante iniziale venga attribuito convenzionalmente il valore 1, che
raddoppia la propria numerosità dopo ogni intervallo di tempo unitario.
Dopo 50 anni Napier, prendendo spunto dagli studi effettuati da Stifel
approfondisce l’idea di logaritmo, questa volta come progressione
geometrica di ragione 10.
John NAPIER ( Edimburgo - Scozia,1550-1617) Barone di Merchistone,
era un matematico dilettante, che principalmente si dedicava a questioni
teologiche e religiose, ma che consegnò il suo nome alla fama per le sue opere sui
logaritmi e sulla geometria e trigonometria . Fu egli a coniare il termine logaritmo (dal
greco: lògon [ragione, intesa qui nel senso usato nelle progressioni geometriche, cioè
rapporto] e arithmòs [numero]: numero razionale, nel senso di numero "artificiale",
creato dalla ragione).
La sua discussione sui logaritmi appare nella celebre opera "Mirifici logarithmorum
canonis descriptio" del 1614.
Con essa egli sperava di fornire uno strumento che rendesse molto più veloci i
calcoli degli astronomi. Laplace, 200 anni dopo, riconobbe il successo di questo
intendimento, scrivendo che il lavoro di Napier "aveva raddoppiato la vita agli
astronomi".
Consideriamo le seguenti successioni di numeri ed i corrispondenti logaritmi (che
non sono altro che gli esponenti delle corrispondenti potenze di 10):

Logaritmi :
0
1
2
3
4
5
Numeri :
Per avere il prodotto di due numeri della seconda successione (progressione
geometrica), basta fare la somma dei due corrispondenti della prima e poi trovare il
numero della seconda che corrisponde a tale somma.
(ad esempio: ) .
Analogamente una divisione può diventare una sottrazione.



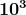





Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor



