



Tu sei giovane solo una volta, ma puoi essereimmaturo per sempre.
Radici ed equazioni algebriche

… studiare, studiare ed ancora
studiare, è il solo modo di capire
quanto possa essere grande
la propria ignoranza!



È interessante notare che, nel campo dei complessi, il numero di
radici (dall'esempio almeno fino a n=3) sembra essere uguale
all'indice della radice stessa. Cioè, data la n√x , avremmo per
n = 2 due radici, per n = 3 tre radici.
Se così fosse e se questa congettura fosse vera per ogni n,
la situazione sarebbe più soddisfacente rispetto a quanto accade
in campo reale, in cui n√x non ha soluzioni se n è pari e x < 0,
oppure ha 1 soluzione se n è dispari e due se n è pari e x >0.
D'altra parte l'estrazione di radice di indice n è in qualche modo
correlata all'esistenza di soluzioni (che non a caso chiamiamo
radici) di equazioni algebriche di grado n, come
I coefficienti e la variabile x sono, nel caso più generale, numeri complessi.
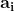
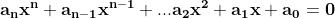
Ad esempio, , equivale a risolvere l'equazione di secondo grado
,
da cui si ottengono le due soluzioni reali .
L'estrazione della radice cubica di
, , significa risolvere l'equazione di
terzo grado
, con l'unica soluzione reale
.
L'estrazione della radice quarta, equivale a risolvere l'equazione di quarto
grado
.
Quest'ultima è un'equazione bi-quadratica che può essere risolta con la nota tecnica
della sostituzione di variabile:
se poniamo
l'equazione diviene:
, che, come prima, dà le soluzioni
reali:
.
L'equazione di quarto grado equivale allora alle due equazioni di secondo grado :
la prima delle quali ha le due soluzioni reali
.
La seconda equazione invece non ha soluzioni nel campo dei numeri reali.
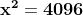
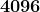
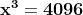
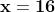
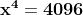
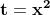
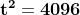
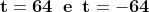
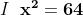
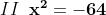
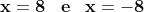
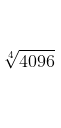
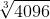

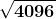
La chiusura algebrica, ovvero quanti tipi di numeri ci vogliono?
Il fatto che esistano equazioni non risolubili , o operazioni non eseguibili all'interno di
una certa struttura algebrica (si direbbe in linguaggio tecnico che la struttura non è
algebricamente chiusa) costituisce una forte motivazione per l'introduzione di nuovi
tipi di numeri. Il campo dei reali non è chiuso per l'estrazione di radice quadrata
perchè questa operazione non è eseguibile per numeri reali negativi. Il campo
complesso è invece chiuso per questa operazione.
Nuovi tipi di numero sono stati introdotti nel tempo per risolvere problemi di chiusura
algebrica:
i numeri interi relativi (Z) risolvono il problema di sottrazioni tipo 3− 5, impossibile
all'interno dei numeri interi naturali (N);
i razionali (Q) permettono la divisione tra interi non divisibili, es. 3 : 5;
con i reali (R) si affrontano questioni più delicate quali l'esistenza di numeri
irrazionali (come
) e di numeri trascendenti come e, numero di nepero, o
, pi
greco, rapporto tra circonferenza e raggio;
i numeri complessi (C) sono la chiusura algebrica dei numeri reali. Un teorema la cui
dimostrazione esula dallo scopo di questa lezione, dettoteorema fondamentale
dell'Algebra, assicura che tutte le operazioni e tutte le equazioni algebriche sono
risolubili in campo complesso e quindi non è e non sarà più necessario ricorrere a
nuovi tipi di numeri.

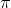
Radice n-sima di un numero complesso
Cerchiamo ora di dimostrare che è possibile estrarre la radice di indice n intero di un
numero complesso con n qualsiasi e che il numero di queste radici coincide con
l'indice n.
Per questo è utile ricorrere alla rappresentazione trigonometrica dei numeri
complessi.
In un precedente paragrafo, abbiamo dimostrato la validità dell'importante
formula di De Moivre:
grazie ad essa è possibile esprimere la potenza
intera di un numero
complesso come:
in cui z è il modulo del numero complesso ed è sempre
positivo.
Immaginiamo ora di calcolare la radice
di e che questa
radice sia z:
allora
e cioè:
perchè questa uguaglianza sia verificata è necessario che: e che
e .
Tuttavia sappiamo che le funzioni trigonometriche seno e coseno sono periodiche
con periodo
per cui dovremo avere:
Da questa equazione ricaviamo:
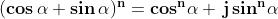
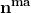
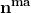
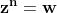
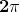
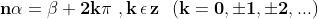
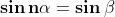
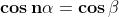
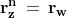
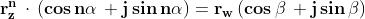
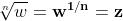
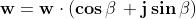

Se
, avremo valori di
che si ripetono, e qundi radici non distinte.
Se, ad esempio, diamo a k il valore n, abbiamo e quindi
che è ancora uguale a . Allora per avere radici distinte il valore massimo di k
sarà n −1, dato che per k = n avrei una radice già trovata con k = 0.
Se considero i valori negativi, ad esempio k= −1, avrò , che però è
uguale a , valore che ottengo anche con
.
Proseguendo si può facilmente verificare che il valore di " per k = −2 si può ottenere
anche per k = n −2. Quindi possiamo limitarci ai valori positivi di k.
Ogni numero complesso possiede allora n radici distinte, così espresse:
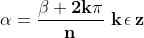
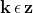
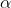
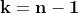
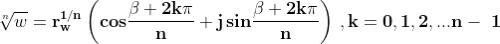
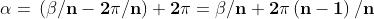
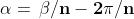
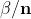
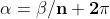
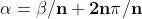
Le radici dell'unità
Come abbiamo visto, l'unità in campo complesso è il numero 1 = 1 + j 0, oppure la
coppia (1,0).
Se:
, allora z rappresenta le radici n-sime dell'unità
La formula precedente dà in questo caso ( ):
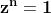
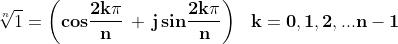
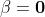


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor



