



Un tempo era grande il rispetto per una testa ricoperta di capelli bianchi.
Elevamento a potenza dei numeri complessi

… studiare, studiare ed ancora
studiare, è il solo modo di capire
quanto possa essere grande
la propria ignoranza!




Elevamento a potenza di numeri complessi. Formula di De Moivre.
Dopo aver preso in considerazione le operazioni fondamentali tra numeri complessi
ci chiediamo ovviamente se e in che modo sia applicabile ad essi il concetto di
elevamento a potenza.
Potenza con esponente intero di un numero complesso
Elevare un numero reale a alla potenza n significa come sappiamo moltiplicare a
per se stesso n volte:

Estendiamo questa definizione ai numeri complessi:
e supponiamo valide le note proprietà delle potenze:
Tutto ciò diventa particolarmente interessante se il
numero complesso è espresso in forma trigonometrica :
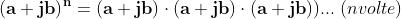
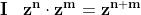

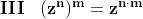
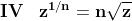
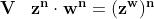

Qui abbiamo applicato la propietà V delle potenze:
la potenza di un prodotto è uguale al prodotto
delle potenze.
Le proprietà del numero cos " + j sin $
Il numero , che chiameremo u, gode di
alcune proprietà interessanti sulle quali vale la pena
di soffermarsi.

Intanto esso rappresenta, al variare di
, qualsiasi numero complesso di modulo unitario, infatti .
Poi, proprio perchè il modulo è unitario, esso può essere considerato alla stregua di un operatore di rotazione di
radianti.
Verifichiamolo con un esempio
Sia , quindi
Moltiplichiamo ora un numero complesso , ad esempio , per :
Poichè , osserviamo che 93.69 − 33.69 = 60°., mentre ovviamente il modulo non è variato.
La moltiplicazione per ha quindi provocato la rotazione di radianti del vettore in senso
antiorario. Questo è un fatto di ordine generale e lo si può facilmente verificare.
L'operazione inversa, cioè la divisione per , ha invece l'effetto di provocare una rotazione in senso
opposto di radianti come è facile verificare.
La forma polare è evidentemente: .


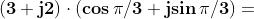
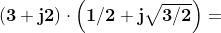




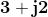


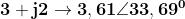

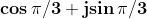
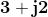

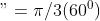
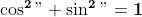
La formula di De Moivre (cos " + i sin ")n = cos n" + i sin n"
Ancor più interessante è il risultato dell'elevamento alla potenza n-sima, con n intero:
Proviamo per ora a calcolare :
Dalla trigonometria sappiamo che:
e
, sono cioè le cosiddette formule
di duplicazione.
Allora abbiamo dimostrato la formula di De Moivre almeno per il caso n = 2:
È relativamente semplice dimostrarne la validità anche per n=3,4,..., tuttavia poichè non possiamo procedere
indefinitamente con queste verifiche dobbiamo cercare una dimostrazione generale della formula.

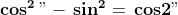
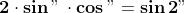
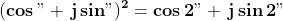


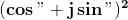

Dimostrazione per induzione della formula di De Moivre
Esiste una tecnica di dimostrazione matematica molto potente: la dimostrazione per induzione.
Si procede così:
Si dimostra l'affermazione per un caso particolare, ad esempio n=1;
Si dimostra che se l'affemazione vale per un caso generico n, allora sarà valida anche per n+1;
Si conclude che, potendo essere n qualsiasi, l'affermazione è vera in generale e con ciò essa risulta dimostrata.
Applichiamo la procedura al nostro caso:
Dobbiamo dimostrare che:
a. per n=1, è certamente vera;
b. supponiamo che , per n qualsiasi, sia vera, dimostriamo che allora lo è anche
per n+1:
Per la proprietà I delle potenze :
ma abbiamo ipotizzato che , quindi:
Per semplicità poniamo , allora abbiamo:
Applicando la definizione di prodotto:
Quindi abbiamo dimostrato che:





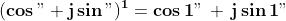


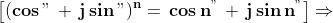
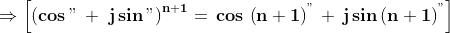

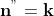

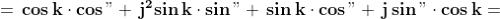


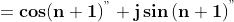
è dimostrata.
In generale allora la potenza n-sima, con n intero, di un numero complesso potrà essere espressa come:

c.
Poichè non abbiamo posto alcuna restrizione su n, esso può assumere
qualsiasi valore e quindi la formula di De Moivre:



Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor



