



Diventare vecchi è obbligatorio - crescere è opzionale.
Forme trigonometriche e polari

… studiare, studiare ed ancora
studiare, è il solo modo di capire
quanto possa essere grande
la propria ignoranza!




Forma trigonometrica e polare dei numeri complessi
Oltre alla forma algebrica a +ib di un numero complesso, sono
possibili altre due importanti forme rappresentative dei numeri
complessi: la forma trigonometrica e la forma polare.
Ricordiamo il significato di alcuni simboli:
è il modulo del numero complesso
ed anche del vettore che lo rappresenta nel piano di Gauss.
Il modulo rz coincide con il raggio della circonferenza su cui

muoviamo il punto z.Ora immaginiamo di proiettare il vettore z sull'asse reale.
Il vettore forma l'angolo " con l'asse reale, l'angolo " è detto argomento del numero
complesso z, si indica con Arg(z) e a volte è anche chiamato angolo di fase o
semplicemente fase.
La proiezione, grazie alle relazioni trigonometriche di un triangolo rettangolo è data
da .
Allo stesso modo proiettiamo z sull'asse immaginario. Questa proiezione è data da
. Ma e , quindi:
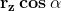


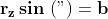
La forma trigonometrica del numero complesso z è allora:
La rappresentazione in forma trigonometrica dei numeri complessi non è univoca,
infatti, a causa della periodicità delle funzioni seno e coseno, si ha anche:



Se si vuole evitare questa ambiguità si può considerare , nel qual caso
prende il nome di determinazione principale di e talvolta si indica con .
Il complesso coniugato di z è:
Possiamo ora dimostrare quanto visto nel paragrafo precedente relativamente a
prodotto e divisione.
La forma trigonometrica per il numero w di modulo w e argomento β è:
w = rw·[cos(β) + jsin(β)]
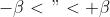

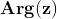


Prodotto di numeri complessi in forma trigonometrica
Il prodotto si ottiene applicando le
definizioni viste precedentemente:
z·w = rz·rw·{ [cos(")cos(β) − sin(")sin(β)] + j·[sin(")cos(β) + cos(")sin(β)] }
se osserviamo le espressioni in parentesi quadre vediamo che
cos(")cos(β) − sin(")sin(β) = cos(" + β) e sin(")cos(β) + cos(")sin(β) = sin(" + β)
e quindi
z·w = rz · rw · [ cos(" + β) + j·sin(" + β)]
Concludiamo che il prodotto è un vettore che ha come modulo il prodotto dei moduli
e come argomento la somma degli argomenti
Divisione di numeri complessi in forma trigonometrica
Per ottenere il quoziente
z/w = (rz/rw)·[cos(") + jsin(")]·[cos(β) + jsin(β)
calcoliamo prima [cos(β) + jsin(β) reciproco di cos(β) + jsin(β).
Applichiamo le definizioni di reciproco date in precedenza:
[cos(β) + jsin(β) = cos(β) / (cos(β + sin(β ) − jsin(β) / (cos(β + sin(β )
ma ricordiamo che (cos(β + sin(β = 1 e allora: [cos(β) + jsin(β) = cos(β) −
jsin(β).
Quindi: z/w = (rz/rw)·[cos(") + jsin(")]·[cos(β) − jsin(β)]











Il quoziente dei due numeri complessi è dato allora da:
z/w = (rz/rw)·{ [cos(")cos(β) + sin(")sin(β)] + j·[sin(")cos(β) − cos(")sin(β)] }
Qui, tra parentesi quadre abbiamo le formule trigonometriche di sottrazione, per cui:
z/w = (rz/rw)· [cos(" − β) + j.sin(" − β)]
Il quoziente è un vettore che ha come modulo il quoziente dei moduli e come
argomento la differenza degli argomenti.


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor



