



Solo i morti e gli stupidi non cambiano mai opinione..
SENO E COSENO

… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!

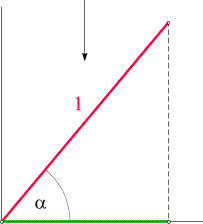
Poniamoci un problema:
Abbiamo un bastone di lunghezza 1 inclinato di un
angolo
rispetto al piano orizzontale, quanto è lunga
la sua ombra quando il sole lo illumina verticalmente?
Si consideri lil disegno sottostante:
Il segmento rosso rappresenta il bastone, la freccia
rappresenta la luce che cade dall'alto.
L'angolo
può essere scelto arbitrariamente
(nell'esempio a lato abbiamo
= 51°).
Si cerca la lunghezza del segmento verde.




A questo punto si ha una sorpresa che pone lo studente
in una situazione completamente nuova.
Il problema non è solubile con le operazioni di calcolo che
abbiamo visto fino ad ora!
Solo in casi eccezionali la lunghezza dell'ombra può
essere espressa con numeri già noti (ad esempio
per
= 60° la lunghezza è 1/2, per
= 45° è 2-1/2),
mentre se prendiamo
= 51° otteniamo un numero
(reale) che non si esprime in questo modo né in modo
simile.




Pur non sapendo come calcolare la lunghezza dell'ombra per
= 51° (a titolo di esempio), è chiaro che questa è univocamente
determinata dalla domanda posta sopra.
Per avere una prima approssimazione, possiamo fare un
disegno (possibilmente) preciso sullo stile di quello riportato
a lato e misurare la lunghezza del segmento verde.
Troveremo un valore di circa 0.63.
Un procedimento di questo tipo è però insoddisfacente dal punto
di vista matematico.
Quello che in ogni caso possiamo fare intanto è dare un
nome al risultato esatto: lo chiamiamo coseno.
La lunghezza del segmento verde si esprime con cos
oppure
cos(
) e si legge "Cosen alpha" oppure "Coseno di alpha".



Poiché l'ombra è la lunghezza dell'immagine che il sole "proietta" sulla terra,
possiamo anche dire: cos
è la lunghezza della proiezione di un segmento che è
inclinato di angolo
e ha lunghezza 1.


Se
= 51°, come nel nostro esempio, scriveremo cos(51°). Il simbolo cos(51°)
rappresenta quindi un numero reale (circa uguale a 0.63), cos(60°) rappresenta un
altro numero reale (e cioè 1/2), ecc.
Analogamente possiamo illuminare il bastone con un raggio
di luce in direzione orizzontale e chiederci quanto sarà lunga
la sua ombra proiettata su una parete verticale.
Anche questa lunghezza in generale non può essere espressa
con uno dei metodi di calcolo a noi già noti.
La chiameremo Seno.
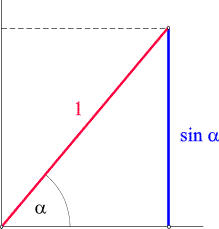
La lunghezza del segmento blu nello schizzo qui a fianco a
destra si esprime con sin
oppure sin(
) e si legge
"Sen alpha" oppure "Seno di alpha".
Anche questa volta si tratta di una proiezione, adesso però ad opera di un raggio di
luce orizzontale. Possiamo anche interpretare sin
come la lunghezza apparente
del bastone rosso sullo sfondo visto da una grande distanza.
Se ad esempio abbiamo
= 51°, scriviamo sin(51°).





Seno e Coseno (ed altre grandezze che vedremo) si chiamano funzioni
trigonometriche.
Il nome "funzione" deriva dal fatto, che a ciascun angolo α possiamo assegnare i
due numeri sin
e cos
.
Quando assegniamo a un numero x il suo quadrato scrivendo f(x) = x2 non facciamo
niente di diverso.
La differenza rispetto a formare il quadrato consiste soltanto nel fatto che il calcolo
numerico di sin
e cos
per un angolo dato
è più complicato.
Per fortuna possiamo delegare questo compito a strumenti come il computer o il
calcolatore tascabile.
Anche questi strumenti per la maggioranza degli angoli ci forniscono solo dei valori
approssimati che però, come nel caso dell'estrazione di radice, sono
sufficientemente precisi per quanto riguarda le nostre più comuni applicazioni
pratiche.





Seno e Coseno, così come tutte le altre funzioni trigonometriche che imparerete a
conoscere in questo capitolo, hanno un ruolo essenziale in matematica e in molte
applicazioni.
Fondamentalmente la loro importanza deriva dal fatto che nascono da problemi
geometrici semplici e molto generali (nel senso che si presentano frequentemente).
Che il calcolo numerico sia complicato e venga quindi delegato al computer o al
calcolatore tascabile non dovrebbe distogliere dalla loro sostanziale semplicità.
SENO E COSENO IN UN TRIANGOLO RETTANGOLO

In linea di massima, adesso abbiamo un'idea di che cosa siano
il Seno e il Coseno di un angolo e vogliamo vedere come li
possiamo utilizzare.
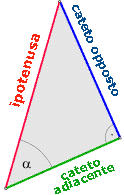
In ognuno dei disegni del paragrafo precedente troviamo un
triangolo rettangolo: l'abbiamo riportato nella figura a destra.
Inoltre abbiamo ruotato leggermente il tutto, visto che la
posizione del triangolo nel piano non ha nessuna importanza.
Con l'aiuto di questo disegno possiamo caratterizzare le due
funzioni trigonometriche in maniera diversa.
In un triangolo rettangolo la cui ipotenusa ha lunghezza 1,
sia
uno dei due angoli acuti. Allora abbiamo che:

•
sin
è la lunghezza del cateto opposto
all'angolo
•
cos
è la lunghezza del cateto adiacente
all'angolo
.




Adesso consideriamo un triangolo rettangolo con lo stesso angolo α,
ma con un' ipotenusa di lunghezza non necessariamente uguale a 1.
Lo otteniamo "dilatando" o "riducendo" il nostro triangolo originale
in maniera tale da mantenere gli angoli.
Si dice che il triangolo originale e quello riportato qui a fianco a
sinistra sono simili.
In entrambi i triangoli, il cateto opposto all'angolo α) (blu) è più corto
rispetto all'ipotenusa di un fattore sin
, e in entrambi i triangoli,
il cateto adiacente all'angolo (verde) è più corto rispetto all'ipotenusa
di un fattore cos
.
In questo senso sin
e cos
possono essere interpretati come
fattori di riduzione.
Ciò può essere dimostrato formalmente grazie al teorema di Talete.
Vediamo quindi che in ogni triangolo rettangolo vale




sin =
cateto opposto
ipotenusa (1)
cos =
cateto adiacente
ipotenusa (2)





Vogliamo illustrare come si utilizzano queste proprietà nei calcoli.
Consideriamo il seguente problema geodetico:
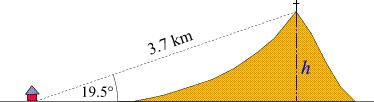
Come raffigurato nella figura a destra,
la distanza diretta fra un punto di
osservazione e la vetta di un monte
misura 3.7 km.
La vetta appare dal punto di osservazione
sotto un angolo di 19.5°. Quanto è alta la montagna?
Soluzione:
Avete trovato il triangolo rettangolo nello schizzo?
Usiamo la relazione (1):
sin (19.5°) =
h
3.7 km

Quindi h = sin(19.5°) × 3.7 km.
Utilizzando un normale calcolatore o delle tabelle di un prontuario, otteniamo
sin(19.5°) = 0.3338, e quindi h = 0.3338 × 3.7 km = 1.24 km, arrotondando
il risultato ragionevolmente.




Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor



