



L’arte di essere saggi è l’arte di capire a cosa si può passar sopra.
LE FUNZIONI ED I DIAGRAMMI

… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!

Si definisce come funzione una relazione tra una
variabile dipendente Y ed una variabile indipendente X
Ad esempio è una funzione la relazione :
Ad ogni valore che si attribuisce alla variabile x ne
corrisponde uno della variabile y.

Le funzioni possono essere rappresentate graficamente
su un piano cartesiano, costituito da due assi orientati
( cioè hanno una freccia che ne indica il verso),
perpendicolari tra di loro (cioè formanti un angolo di 90°).
I due assi vengono chiamati:
x asse delle ascisse
y asse delle ordinate.
Il punto in cui si incontrano i due assi prende il nome di origine degli assi.
In una rappresentazione cartesiana si parla SOLO di coppia di numeri ( x ed y); ad
ogni coppia corrisponde un punto sul piano cartesiano e, viceversa, ad ogni punto
sul piano cartesiano corrisponde una coppia di numei, detti ascissa ed ordinata del
punto. I due numeri sono detti le coordinate del punto.
Ad esempio :
Per rappresentare i punti sul piano è indispensabile stabilire una unità di misura.
Genericamente chiamiamo u l'unità di misura ed essa potrebbe corrispondere ad 1
quadretto del vostro quaderno od ad 1 cm., oppure ad una qualsiasi altra unità di
misura; l'importante è quello di determinarla come una costante, in modo da rendere
omogeneo il grafico.
Proviamo adesso a tracciare il grafico che rappresenta la funzione :
e
per questo è necessario trovare una serie di punti che, uniti tra di loro, possano
fornire la linea cercata.


Scegliamo dei valori arbitrari per la x e calcoliamo i corrispondenti valori di y :
per x=0 si ha : y=(3x0)-2 = -2
per x=1 si ha : y=(3x1)-2 = 1
per x=2 si ha : y=(3x2)-2 = 4
Questi valori si possono riassumere in una tabella del tipo:

ed in questo modo si ottengono le coordinate dei punti :
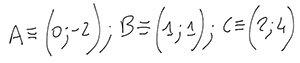
Dopo aver determinato l'unità di misura u, questi punti possono essere rappresentati
come segue:
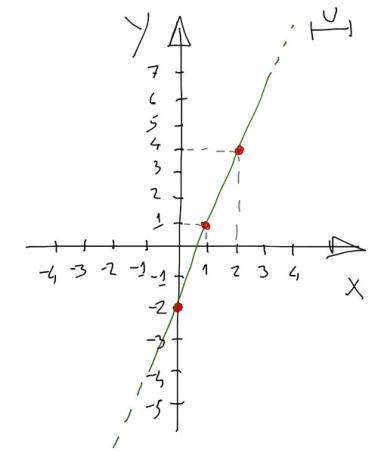
Il grafico così ottenuto è una retta.
Questa breve introduzione mi pare sufficiente per affrontare le lezioni seguenti....


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor



