



Un governo d'onesti è come un bordello di vergini
Metodi Grafici per il rilievo delle Traiettorie degli Elettroni


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!






Metodi grafici per il rilievo delle traiettorie
degli elettroni
I metodi sperimentali considerati nello studio della
distribuzione del campo elettrico permettono, nella mag-
-gioranza dei casi, il tracciamento delle linee equipotenziali
nei piani di simmetria.
Il problema della determinazione delle traiettorie degli
elettroni dovrà essere necessariamente risolto con metodi
grafici.
Le costruzioni che verranno descritte si riferiscono a
metodi di estrema semplicità' ma approssimati; l'attendi-
-bilità dei risultati è soddisfacente se i salti di potenziale
tra successive linee equipotenziali sono piccoli nei confro-
-nti delle tensioni di alimentazione applicate tra gli elettrodi.
a)
Metodo del raggio di curvatura.
L'approssimazione del metodo del raggio di curvatura consiste nel rappresentare con un
arco di cerchio la traiettoria di un elettrone tra due linee equipotenziali consecutive.

Costruzione della traiettoria di un elettrone in un campo elettrico a potenziale crescente
Supponendo che un elettrone parta da un punto A con velocità iniziale Va, si consideri,
riferendoci alla soprastante figura, la linea equipotenziale passante per A, la successiva cor-
-rispondente al potenziale e la distanza d tra le due curve, valutata secondo
la direzione normale s.
Si scomponga la forza
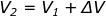
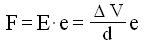
Che il campo elettrico E esercita sull'elettrone posto in A, nelle due forze:
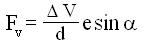
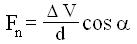
agenti rispettivamente nella direzione delle velocità Va e secondo la normale n-a-Va.
Per efferto di questa ultima la traiettoria si incurva discostandosi dalla direzione della
velocità iniziale.
Il raggio di curvatura D del. tratto della traiettoria che interessa tracciare mediante un
arco di cerchio, può essere determinato tenendo conto che, nel moto dell'elettrone la
componente Fn e' equilibrata dalla forza centrifuga.
Dalle relazioni e si ottiene
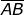



Mentre la direzione della velocità è individuata dala tangente alla traiettoria nel
punto B, il valore assoluto è determinato dalla relazione:
dal quale si ottiene
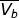

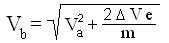
Determinato il centro di curvatura O e raggiunta in B la successiva equipotenziale si
procede successivamente nello stesso modo sino al raggiungimento della traiettoria
completa.
b)
Metodo di Descartes
La traiettoria di un elettrone in un campo elettrico e' paragonabile al percorso di un
raggio luminoso in un mezzo ad indice di rifrazione variabile.

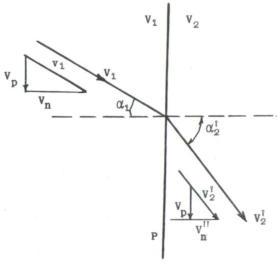
Rifrazione di un elettrone attraverso una barriera
di potenziale
E' noto infatti che un elettrone può' essere rifratto,
riflesso o focalizzato analogamente a quanto
avviene per una sorgente luminosa.
In particolare, se un elettrone incide con una
certa velocità V1 su un piano ideale che separa
lo spazio in regioni caratterizzate da valori
costanti diversi dal potenziale elettrico, oltrepas-
sando la barriera di potenziale aumenta (V2 > Vi)
o diminuisce (V2 < Vi) la propria forza viva, come
simboleggiano le due figure alla tua sinistra.
Mentre in entrambi i casi rimane inalterata la
componente tangenziale Vp della velocità, la
componente normale Vn aumenta o diminuisce a
seconda che sia V2 > Vi o viceversa.
Si può quindi concludere che quando un elettrone
attraversa una barriera di potenziale subisce un
fenomeno di rifrazione e la traiettoria si avvicina
(V2 > Vi) o si allontana (V2 < Vi) dalla normale
in analogamente a quanto avviene per un raggio
luminoso che entri in un mezzo di maggiore o
minore densità.
Indicando con "1, l'angolo di incidenza e con "2
l'angolo di rifrazione dovendo risultare
Vp = V1 sen "1 = V2 sen "2, si ottiene la
relazione:

Tenendo conto che la velocità di un elettrone dipend dalla radice quadrata del potenziale, la
soprastante relazione può essere scritta nella forma :
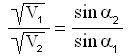

Tracciamento della traiettoria di un elettrone con il metodo di Descartes
Il metodo di Descartes si avvale della legge della rifrazione ed è, come del resto anche il
precedente, un metodo approssimato perchè considera costante il potenziale dello spazio
delimitato da due successive linee, rappresentandolo con la media dei valori che si riferiscono
alle due linee equipotenziali considerate.
La traiettoria è di conseguenza determinata da una successione di segmenti
rettilinei.
La soprastante figura si riferisce al percorso di un elettrone in un campo a potenziale
crescente.
Se si suppone che un elettrone incida nel punto B sulla linea a potenziale V2
provenendo da una regione ideale a potenziale costante Vm1 = (V1+V2)/2, la
relazione:

permette di calcolare il valore dell'angolo di rifrazione "2 necessario per rappresentare con
il segmento la traiettoria tra le linee equipotenziali di parametri V2 e V3.
Come indica la soprastante figura, la direzione può' anche essere determinata
considerando un qualsiasi arco di cerchio di centro B, il suo punto T di intersezione
con il prolungamento del segmento ed i seguenti normali a e essendo questo
ultimo di lunghezza tale che :
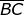
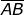
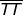

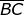
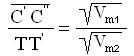


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor



