



Esiste sempre qualcuno che desidera esattamente quello che desideri tu
TRAIETTORIA DEGLI ELETTRONI


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!









1)Generalità
Lo studio dei tubi termoionici consiste principalmente nello
stabilire quale sia la traiettoria degli elettroni che si
spostano nel campo elettrico generato dagli elettrodi in
funzione della forma e dimensioni di questi.
Quando la forma e la posizione dei vari elettrodi corrispo-
-ndono a disposizioni geometriche particolarmente semplici
il problema descritto e' di facile soluzione ma spesso le
difficoltà sono tali che si rende necessaria una determina-
-zione sperimentale dell'andamento delle linee di forza e
delle superfici equipotenziali del campo elettrico.
2) Comportamento di elettroni isolati in campi
elettrici particolarmente semplici.
a)
Campo elettrico uniforme e velocita' iniziale nulla

Supponendo che un elettrone parta dalla
posizione A rappresentata nella figura a
lato, con velocita' iniziale nulla,ed assu-
-mendo come senso positivo degli
spostamenti X e della velocita' V quella
propria del campo elettrico, per la seconda
legge di Newton si ha:
[a]
dove :
m =
la massa di un elettrone in Kg
e =
la carica di un elettrone in Coulomb
x=f(t)
la posizione dell'elettrone al tempo t, in m.
t =
il tempo in secondi
e=-(dv/dx)
la costante dell'intensità del campo elettrico
-Ee= la forma agente sull'elettrone
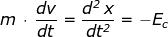

da cui :
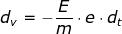
ed integrando rispetto al tempo, essendo nulla la velocità iniziale, si ottiene :
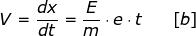

ed attraverso una seconda integrazione :

Come indicano le relazioni [a], [b] e [c], il moto dell'elettrone
è uniformemrnte accellerato
la velocità diretta nel senso dei potenziali crescenti è funzione lineare del tempo.
Dalla relazione [c], eliminando la variabile tempo, si ottiene:
ed essendo per la [b]

ne risulta


Indicando con V=f(x) la differenza di potenziale E(x0-x), tra i punti di ascissa x0 ed x,
la relazione [d] diviene:
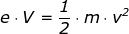
da cui risolvendo rispetto a v2 e v :
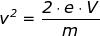

b)
Campo elettrico uniforme e velocita' iniziale (-v0) negativa e parallela alla
direzione del campo.
La relazione [b] diviene

da cui:
Dovendo essere verificata la relazione:
da cui:

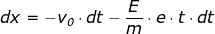
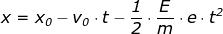



ma poichè indicando con V0 la velocità v0 espressa convenzionalmente in Volts, si
ha
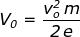


e
Il moto dell'elettrone è, come nel caso precedente un moto uniformemente accellerato
c)
Campo elettrico uniforme e velocita' iniziale (v0) positiva e parallela alla
direzione del campo.
Le precedenti relazioni divengono :
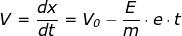

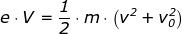

Come indica la relazione [f] il moto è uniformemente ritardato e la velocità si annulla
ad un valore t1 di t che rende nullo il secondo membro della relazione [e].
Di conseguenza:
[f]
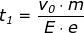
corrisponde all’ascissa

Successivamente l'elettrone riparte dal punto di ascissa x1 in senso contrario e con
moto uniformemente accellerato
d)
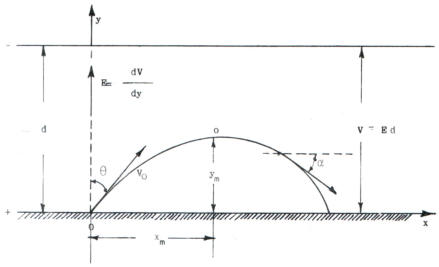
Campo elettrico uniforme e velocita' iniziale non parallela alla direzione del campo.
Quando un elettrone entra in un campo elettrico uniforme con una velocità iniziale
che forma un angolo diverso da zero con la direzione del campo elettrico, l'elettrone
segue una traiettoria parabolica.
La figura a lato si riferisce ad un campo
elettrico uniforme con azione ritardatrice
ed il caso esaminato è analogo a quello
che si riferisce al moto di un proiettile
che in assenza di attrito sia soggetto alla
forza di gravità.
Indicando con Vx e Vy le componenti
della velocità secondo gli assi cartesiani,
poichè la forza elettrica -Ee che agisce
sull'elettrone uscente dal punto 0 ha
componente nulla sull'assex e le equa-
-zioni differenziali del moto divengono:

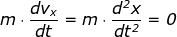
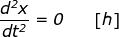
ossia
Le condizioni ai limiti che rendono determinate le soluzioni del problema sono le
seguenti :
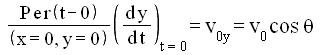

Come risultato di una prima integrazione rispetto al tempo delle relazioni [g] ed [h], si
ottiene :
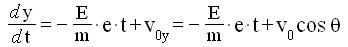
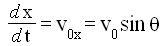
e da una seconda integrazione :
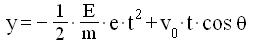
[i]

[l]
dalla relazione [l], si ottiene :
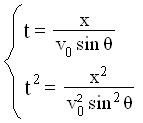
e sostituendo i valori ottenuti nella [i]:

[m]
Quest'ultima equazione rappresenta un parabola. Esprimendo convenzionalmente la
velocità in Volt, si ha :
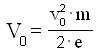
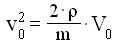
ad
la relazione [m] può essere scritta nella forma:
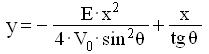
[n]
ed il punto più alto sulla traiettoria ha le coordinate:
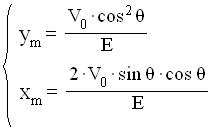
Con riferimento alla figura di cui sopra, essendo E=V/d, la relazione[n] diviene:

Considerato che a parità di angolo θ e la distanza d degli elettrodi che danno origine
al campo elettrico, la pendenza della traiettoria dipende unicamente dal rapporto
V/V0, può essere affermato il seguente principio :
"Se in un sistema puramente elettostatico sono fatte variare tutte le tensioni nello
stesso rapporto, rimangono immutate le triettorie degli elettroni."


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor



