



Rilassati e svuota la mente, non dovrebbe essere difficile per te.!
VALOR MEDIO ED EFFICACE


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!








VALORE MEDIO E VALORE EFFICACE NELLE CORRENTI ALTERNATE
Valore efficace
Nella pratica tecnica si usa commisurare la intensità di una
corrente alternata a quella di una corrente continua termi-
-camente equivalente. A tale scopo si definisce come
valore o intensità efficace di una corrente alternata, quel
valore che dovrebbe avere una corrente costante,
circolante nello stesso circuito,
per produrre nel corso di ogni
periodo la stessa quantità di
calore. Se si pensa che la
potenza elettrica dissipata per
effetto Joule varia proporzio-
-nalmente al quadrato della
corrente, si comprende che
l'energia W dissipata da una
corrente alternata nel corso di
un periodo, si deve esprimere mediante una sommatoria del tipo :
Volendo stabilire l'equivalenza termica con una corrente costante I si deve scrivere
perciò l'eguaglianza :
Dalla quale ne risulta:
e quindi
Si esprime questo fatto dicendo che il valore efficace I di una corrente alternata
corrisponde alla radice quadrata della media aritmetica dei quadrati di tutti i valori
istantanei nel corso di un periodo.

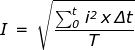
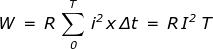

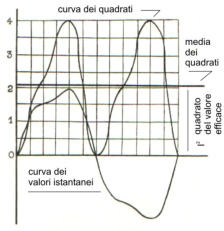
In base a questo risultato, data la forma d'onda di una
corrente alternata qualsiasi, per ricercarne il valore efficace
si deve in primo luogo costruire per punti la curva che ha
per ordinate i quadrati dei valori istantanei come è indicato
nella figura a alto.
(Si noti che i quadrati sono sempre positivi). Dopo di ciò si
deve segnare il rettangolo equivalente all'area racchiusa
dalla curva dei quadrati: l'altezza di questo rettangolo
rappresenta la media di tutti i quadrati ed è eguale perciò al
quadrato del valore efficace della corrente.
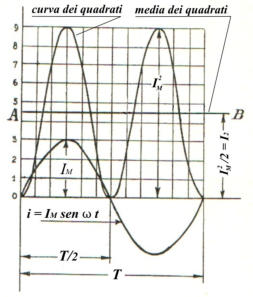
Se si tratta di una corrente di forma sinusoidale, si può
facilmente constatare che la curva dei quadrati è ancora
una sinusoide tangente inferiormente all'asse dei tempi
e avente una frequenza doppia della corrente, com'è
indicato in figura. Posto infatti:

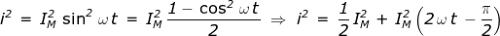
II primo termine di questa espressione è costante e rappresenta perciò una retta
orizzontale A B avente un'ordinata pari a ; il secondo termine invece,
rappresenta un'onda sinusoidale di ampiezza , e di pulsazione , vale a dire di
frequenza doppia di quella della corrente. Ciò significa che la curva dei quadrati dei valori
istantanei della corrente è precisamente una sinusoide di frequenza doppia, che ha per asse
di simmetria la retta A B come mostrato in figura.
Questa stessa retta delimita perciò anche il rettangolo equivalente all'area racchiusa dalla
curva dei quadrati dei valori istantanei, e cioè di quel rettangolo che ha per altezza il
quadrato del valore efficace I della corrente.
Si può dunque affermare che per una corrente di forma sinusoidale, il quadrato del valore
efficace corrisponde alla metà del quadrato del valore massimo: si ha cioè
e cioè




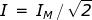
La considerazione del valore efficace si estende praticamente oltre che alle correnti,
anche a tutte le altre grandezze alternative che interessano i circuiti elettrici ed in
particolare alle tensioni. Per tutte le grandezze alternative di forma sinusoidale, il
valore efficace è sempre eguale al valore massimo diviso per √2: per le onde
alternative deformate invece, la ricerca del valore efficace deve essere fatta di volta in volta
costruendo come si è detto l'ordinata media della curva dei quadrati dei valori istantanei.
Nella pratica tecnica quando si esprime l'intensità di una corrente alternata oppure il valore
di una tensione, si intende sempre alludere, salvo esplicita dichiarazione contraria, ai
rispettivi valori efficaci, i quali vengonoindicati sempre con una lettere maiuscola scritta in
carattere normale come I, V, ecc.
Così anche gli strumenti indicatori normali delle correnti e tensioni alternate (amperometri
e voltmetri) forniscono direttamente la misura dei valori efficaci, ciò che è del resto una
conseguenza implicita nello stesso principio di funzionamento di questi apparecchi.
Infatti gli strumenti per corrente alternata devono essere tali da deviare sempre nello stesso
verso anche quando la corrente si inverte; essi devono perciò sfruttare quelle azioni che
variano proporzionalmente al quadrato della corrente, quali sono in particolare l'effetto Joule
(strumenti termici o a filo caldo) e le azioni elettrodinamiche (strumenti elettrodinamici).
Se la frequenza della corrente fosse molto bassa e l'inerzia dello strumento fosse trascura-
-bile, l'equipaggio mobile seguirebbe così le vicende rappresentate dalla curva dei quadrati
dei valori istantanei. All'atto pratico invece l'equipaggio mobile non può seguire le rapide
variazioni periodiche della coppia che lo sollecita, ma si ferma nella posizione di equilibrio
che rimane determinata dalla coppia media. In tal modo la deviazione che si legge sulla
scala viene a dipendere dalla media dei quadrati dei valori istantanei e perciò in definitiva
dal quadrato del valore efficace.
Valore medio

Abbiamo già detto che qualunque grandezza alternativa soddisfa sempre alla condizione di
presentare nel corso di un periodo un valore medio eguale a zero.
Talvolta però interessa considerare il valore medio nell'intervallo
di mezzo periodo: questo valore viene sempre indicato con una
lettera maiuscola munita dell'indice m come Im , Vm, ecc.
Esso corrisponde evidentemente all'ordinata media di una
semionda, come è indicato in figura ed è perciò definito da una
relazione analitica del tipo:


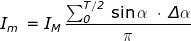

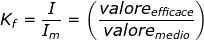
Se l'onda alternativa è di forma sinusoidale, risulta
Con opportuni sviluppi questa ciò fornisce il valore medio.
Nell'espressione del valore medio si possono sostituire i tempi gli angoli descritti del
vettore rotante da cui si deriva la costruzione della sinusoide: poichè il semiperiodo
corrisponde a mezzo giro risulta
Dopo di ciò si deve calcolare la sommatoria o più esattamente l'integrale di sen" x Δ"
fra i limiti zero e B, che risulta eguale a 2.
Si osserva in particolare che il valore medio Im di un'onda sinusoide è minore del
valore efficace: il rapporto fra questo e il primo è infatti
Questo valore è caratteristico delle sole forme sinusoidali: per le onde alternative
deformate invece il rapporto fra il valore efficace ed il valore medio risulta più o
meno diverso da 1,11.
il rapporto
viene perciò designato col nome di fattore di forma.


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor



