



Così è la disperazione, come una preghiera senza destinatario.
GRANDEZZE ALTERNATIVE


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!







GRANDEZZE ALTERNATIVE
Si chiama funzione alternata o alternativa, qualsiasi
funzione del tempo che soddisfi insieme alle due condizioni
di essere periodica e di presentare in ciascun periodo un
valore medio nullo.
La prima condizione stabilisce che la funzione deve
assumere tutta la serie dei suoi valori possibili entro un
determinato tempo T , per poi riprendere ordinatamente
gli stessi valori in tutti gli intervalli successivi eguali a T:
l'intervallo di tempo T costituisce il periodo della funzione
il quale viene misurato in secondi.
La seconda condizione significa invece che l'intera succes-
-sione di valori che la funzione assume in ciascun periodo
deve comprendere dei valori positivi e negativi così
distribuiti nel tempo da condurre ad un valore medio
eguale a zero: una funzione alternata deve quindi neces-
-sariamente cambiar segno in ogni periodo almeno una
volta.
In conformità a queste definizioni si designa col nome di grandezza, alternata, ogni grandezza
fisica variabile nel tempo con legge periodica alternativa, intendendo che al fatto algebrico del
cambiamento di segno, corrisponda il fatto fisico dell'inversione del senso in cui la grandezza
considerata agisce.
Sono grandezze alternate ad esempio gli spostamenti, le velocità e le accelerazioni di tutti i
moti oscillatori: nel nostro studio dovremo considerare in particolare tensioni e correnti
alternate e perciò anche campi magnetici e campi elettrici alternativi.
Gli elementi caratteristici fondamentali di una grandezza alternata sono il periodo e
la forma.
Il periodo di una grandezza alternata può definirsi come l'intervallo di tempo costante che
decorre fra l'istante in cui la grandezza considerata ha un determinato valore e il primo istante
successivo in cui lo riprende dopo aver percorso tutti i valori positivi e negativi che essa può
assumere.
Se il periodo misurato in secondi è T, il rapporto 1/T definisce il numero di periodi al secondo
e cioè la frequenza.
f = 1/T

La frequenza si misura pertanto con l'unità " " che viene
designata hertz (Hz) o periodi al secondo (p/s).
Col nome di forma di una grandezza alternata si designa brevemente
la legge di variazione della grandezza data nell'intervallo di un periodo.
Questa legge può essere definita mediante una funzione analitica del
tempo oppure mediante una rappresentazione grafica, ottenuta
riportando sull'asse delle ordinate del diagramma i valori istantanei
successivi che la grandezza assume in corrispondenza dei tempi
rispettivi rappresentati sull'asse delle ascisse.
Si ottiene una curva continua o discontinua, o eventualmente anche
una spezzata, la quale da una chiara ed efficace immagine della legge
di variazione della grandezza nel tempo.
Da questa rappresentazione è derivata la denominazione di forma
d'onda o curva della grandezza in esame: si intende che il diagramma
può essere limitato ad un solo periodo, perché nei periodi successivi
si ripetono le stesse vicende.Nella figura a lato sono tracciati ad
esempio alcuni tipi di forma d'onda, che si presentano talvolta nella considerazione dei
fenomeni elettrici. Le superfici positive e negative di queste curve hanno talvolta una forma
diversa, ma devono presentare in ogni caso una identica area: ciò in relazione al fatto che il
valore medio nel corso di un periodo deve risultare eguale a zero.
Grandezze alternative sinusoidali.
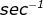
Fra tutte le forme alternative si considera come forma tipica di riferimento la forma
sinusoidale che è definita da una funzione del tipo
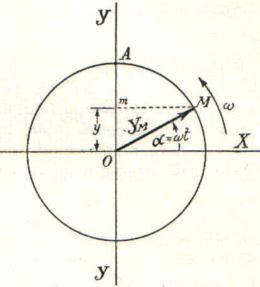
I valori istantanei successivi y di questa funzione variano proprozionalmente al seno di un
angolo uniformemente crescente come l'angolo descritto da un segmento che ruoti attorno
ad un estremo con velocità angolare costante ω: se si
stabiliscono i riferimenti indicati in formula, tali valori
risultano senz'altro rappresentati in grandezza e segno dalle
proiezioni del segmento rotante YM = OM sull'asse diame-
-trale fisso YY. Mentre il segmento rotante descrive il primo
quadrante da 0 a 90° a partire dall'asse di riferimento OX,
la sua proiezione sull'asse YY (Om - y) cresce da zero fino
a ricoprire l'intero raggio OA: il seno dell'angolo descritto
dal segmento varia da zero a uno e la funzione y assume
così tutti i valori a partire da zero fino a raggiungere il valore
massimo YM.
Nel secondo quadrante invece (da 90° a 180°) la proiezione
del segmento rotante decresce dal valore OA a zero: il seno
dell'angolo varia da uno a zero e la funzione y decresce in proporzione da Y^ a zero.
Nel mezzo giro successivo (da 180° a 360°) si ripetono le stesse vicende col segno cambiato,
e così di seguito per tutti i giri successivi.
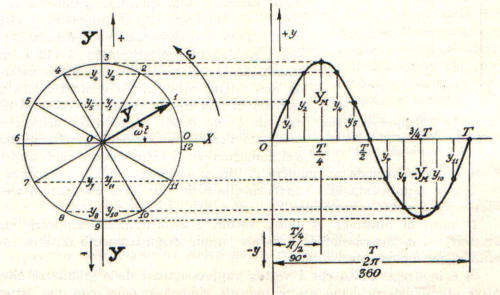
La curva rappresentativa della
funzione y così definita è una
curva sinusoidale di ampiezza
Ym la quale può essere facilme-
-nte costruita nel modo indicato
nella figura a lato.
Il periodo T di questa funzione
corrisponde al tempo impiegato
dal segmento rotante a descri-
-vere un giro completo: se ω
è la velocità angolare espressa
in radianti al secondo, risulta
perciò

L'asse delle ascisse della curva sinusoidale può venire così graduato sia in tempi e cioè in
secondi, sia in angoli misurati in radianti o anche in gradi.
Si dirà perciò che un periodo T corrisponde a radianti o 360°, mezzo periodo a
radianti o 180° e così via.

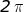
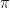


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor



