



Mi sentirò morire dovendo immaginare con chi sei
IL CONDENSATORE IN CORRENTE ALTERNATA (3)


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!





Il Condensatore in regime di Corrente Alternata
(...seguito)
Nel circuito della figura a destra, un condensatore e una
lampada sono collegati
tramite un interruttore
ad una fonte di correnrte
alternata (AC) .
Il condensatore si carica
e si scarica di continuo
seguendo i cambiamenti di polarità dell'alimentazione AC.
La corrente AC scorrerà nel circuito continuamente e la
lampada rimarrà accesa . La freccia rossa e quella blu
indicano le correnti di carica e scarica .Così ' appare ' un
condensatore che sembra consentire ad una corrente
alternata di attraversarlo.
Dico ' sembra ' perché mentre vi è corrente che scorre nel
circuito per tutto il tempo, in nessun momento in realtà


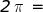

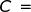


questa fluirà attraverso il condensatore . Ricordate che il condensatore ha un dielettrico
isolante che non farà passare alcuna corrente .
La corrente scorre continuamente nel circuito perché il condensatore viene costantemente
sottoposto alla carica ed alla scarica.
La capacità è la proprietà di un circuito che si oppone a cambiamenti di tensione .
Un condensatore ha pertanto una opposizione al flusso di corrente . L'opposizione al flusso di
corrente prodotta da un condensatore si,come abbiamo già visto, si chiama reattanza
capacitiva e si misura in ohm . La simbologia per reattanza capacitiva è Xc e si determina:

cioè è inversamente proporzionale alla frequenza f della correne alternata ed al valore C della
capacità.
Equazioni per determinare la Xc
Tornamo a prendere in esame l'equazione della reattanza capacitiva:
Tanto più aumenta la frequenza f, più piccola sarà la reattanza
capacitiva Xc ed altrettanto accade all'aumentare della capacità C.

dove:
Reattanza capacitiva in Ohm
il doppio della costante numerica 3,14
Il valore dellafequenza in Hertz
Il valore della capacità in Farad (F)
Osservando l'equazione notiamo che nell'equazione, tutti i termini sono al denominatore e
che è una costante ( non cambia ) .
Possiamo dire quindi che la reattanza capacitiva è inversamente proporzionale alla
frequenza ed alla capacità.
In altre parole , se la capacità (o la frequenza) vengono raddoppiate la reattanza
capacitiva si dimezzerebbe . Se la capacità (o la frequenza) vengono dimezzate, la
reattanza capacitiva risulterebbe raddoppiata, e così via .
Esempio di calcolo .
Un condensatore di 0.05uF è collegato ad una alimentazione AC 10 volt che ha una
frequenza di 500 kHz .
Qual è la reattanza capacitiva in ohm e quanta corrente scorre nel circuito ?
1 / ( 6,2831 x 500 x 103 x 0,05 x 10-6 )
6,366 ohm
La corrente è trovata attraverso l'applicazione della legge di Ohm sostituendo Xc alla R
nell'equazione .
I = V / Xc = 10 / 6,366 = 1.57 Amp


(Ω)
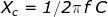
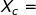
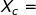

Se vi sono state fornitre le reattanze capacitive in un circuito ed
hai la necessità di trovare il totale netto della reattanza capacitiva,
puoi usare la stessa regola che usi per trovare la resistenza totale
di un circuito. Ad esempio, due reattanze capacitive di 100 ohm in
serie sono pari a 200 ohm ed in parallelo la stessa combinazione
sarebbe 50 ohm.
Per evidenziare ciò che avete imparato,
provate a dare un'occhiata sul circuito raffigurato a lato.
Potremmo dedurre la tensione sui terminali dei condensatori da 1uF e 2uF, utilizzando il
metodo proporzionale. Invece , cerchiamo di capire quanta corrente fluisce nel circuito ,
quindi utilizzando la Legge di Ohm lavoro, determiniamo la tensione ai capi di ciascuno dei
condensatori .
La reattanza del condensatore 1uF è:
Xc1 = 1 / 2Bfc
Xc1 = 1 / ( 6,2831 x 1 x 10^6 x 1 x 10-6 )
Xc1 = 0,159154943 ohm
La reattanza del condensatore 2 uF ( dovrebbe essere la metà perché la capacità è
doppia ) :
Xc2 = 1 / 2Bfc
Xc2 = 1 / ( 6,2831 x 1 x 10^6 x 2 x 10-6 )
Xc2 = 0,079577471 ohm
La reattanza capacitiva totale è la somma delle due reattanze :
Xc (totale ) = Xc1 + Xc2 = 0,159154943 + 0,079577471 Ohm
Xc (totale ) = 0,238732414 Ohm
La corrente che scorre nel circuito è :
I = V / Xc ( totale ) = 900 / 0,238732414 = 3769,911194 ampere
La tensione che grava sul condensatore da il 1uF (dovrebbe essere 600 volt ) :
V = I XC1 = 3.769,911194 x 0,159154943 = 599,9998392 volt

Analogamente, la tensione ai morsetti del condensatore da 2uF
(dovrebbe essere 300 volt ) :
V = I XC2 = 3.769,911194 x 0,079577471 = 299,9999987 volt
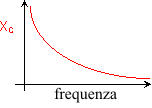
A destra un grafico della Xc verso la FREQUENZA
Come si può vedere dal grafico, all'aumentare della frequenza
la reattanza capacitiva diminuisce .
A destra un grafico della Xc verso la CAPACITA'
Analogamente a quanto sopra, mostra che come la capacità
aumenta Xc diminuisce .
La POTENZA in un circuito capacitivo
La capacità non dissipa energia .
L' unica entità di un circuito che può dissipare energia è la resistenza .
Tutta la potenza presa da un circuito puramente capacitivo durante il ciclo di carica
viene restituito durante il ciclo di scarica .
Quindi una capacità pura non dissipa alcuna potenza .
Nella pratica ogni condensatore ha qualche resistenza nei reofori e nelle armature e
quindi una piccola quantità di potenza viene dissipata .
Sempre in pratica, nei condensatori una piccola quantità di energia viene persa nel
dielettrico, e questa viene chiamata perdita dielettrica. Gli atomi all'interno del
dielettrico di un condensatore sono posti sotto stress e si muovono leggermente a
causa del campo elettrico . Particolarmente a frequenze più elevate , la perdita
dielettrica può diventare significativa .


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor



