



Il giovane che non ha mai pianto è un selvaggio, il vecchio che non ride è uno stolto
IL CONDENSATORE (3)


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!






L'ENERGIA NEI CONDENSATORI
Dove si trova l'energia immagazzinata ?
Anche se abbiamo detto che l'energia è stata memorizzata
dalla carica sulle armature del condensatore, è più corretto
dire che l'energia viene immagazzinata nel campo elettrico
È la carica sulle piastre che forma il campo elettrico tra le
armature . Quando la corrente fluisce in un condensatore,
caricandolo , il campo elettrico diventa più forte (immagaz-
-zina più energia ) . Quando la corrente fuoriesce del
condensatore , la tensione tra le armature diminuisce e
quindi la si manifesta una diminuzione del campo elettrico
( energia fuoriesce dal campo elettrico ) .
UNITÀ DI CAPACITÀ
L'unità di capacità è detta Farad ed il suo simbolo è F.
Il farad misura la capacità dei condensatori di immagazzinare una carica .
Se un volt viene applicata alle armature di un condensatore e questo provoca un immagaz-
-zinamento di carica tra le armature di 1 Coulomb, la sua capacità risulta essere di 1 Farad .
In pratica 1 farad è una enorme capacità, più pratico è l'utilizzo delle sue sub- unità
Microfarad (μF), Nanofarad (nF) e Picofarad (pF); quest sono le sottounità più
comuni .
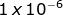

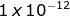
1 microfarad = Farad
1 nanofarad = Farad
1 picofarad = Farad
Permettività o costante dielettrica
Il materiale isolante tra le armature (dielettrico) determina la concentrazione di linee di forza
elettrica. Proprio come materiali diversi si concentrano linee di forza magnetiche di maggiore
o minore entità , materiali variano nella loro capacità di concentrare le linee di forza elettriche
Se il dielettrico è aria, verrà creato un certo numero di linee di forza. Alcune carte hanno una
costante dielettrica due volte quella dell'aria, il che causa la creazione del doppio delle linee
di forza e quindi la capacità risultante risulta essere doppia .
Più alta è la costante dielettrica e maggiore è la capacità risultante, a parità di area
delle armature .
Supponiamo che ad un condensatore avente come dielettrico l'aria (costante dielettrica
abbastanza vicino a 1) della capacità di 8 microfarad, sostituiamo il suo dielettrico di aria s
con un dielettrico di mica , senza modificare la distanza tra le piastre, vediamo la sua
capacità aumentare in modo direttamente proporzionale alla costante dielettrica.
In altre parole , la capacità aumenterebbero da 8 microfarad a 5-7 volte tale valore ,
da 40 a 56 microfarad .
Costanti dielettriche


Materiale
Costante dielettrica
Vuoto
1
Aria
1.0006
Gomma
2 - 3
Carta
2 - 3
Ceramica
3 - 7
Vetro
4 - 7
Quarzo
4
Mica
5 - 7
Acqua
80
Titanato di Bario
7500


FATTORI DETERMINANTI CAPACITÀ
CONDENSATORE PIANO
Consideriamo un condensatore ad armature piane e parallele (condensatore piano), nel quale
i conduttori sono due armature piane, parallele e di area A ad una distanza d.
Se connettiamo le armature ai morsetti si una batteria comparirà la carica + q su una di esse
e la carica - q sull'altra. Se d è piccolo rispetto alle dimensioni delle armature, l'intensità del
campo elettrico tra le armature sarà uniforme.
Per calcolare la capacità dobbiamo trovare la
relazione tra V, differenza di potenziale tra le
armature, e q , carica del condensatore.
Dal teorema di Gauss, essendo il campo E
costante, si ha : ε0 ΦE = q e quindi, essendo ΦE
otteniamo q = ε0 E A dove con ε0 si indica la costante dielettrica di ciò che
si interpone tra le due armature, il dielettrico.
Il lavoro necessario per portare una carica di prova q0 da una armatura all'altra si può
esprimere come L = q0 V oppure come prodotto della forza q0 E per la distanza d, ossia
L = q0 E d Eguagliando le due espressioni avremo V = E d
La capacità sarà
C = q/V = ( ε0 E A) / E d = ( ε0 A )/ d
La relazione trovata mostra che la capacità di un condensatore dipende dalla
geometria dei conduttori (armature) cioè da A e da d.

CONDENSATORE CILINDRICO
Dato un condensatore cilindrico di lunghezza L , costituito da due cilindri coassiali,
rispettivamente di raggio a e b, con L>>b, e carica q sulle armature.
Consideriamo una superficie cilindrica coassiale
con le armature di raggio r e di lunghezza L, con
a<r< b, e applichiamo ad esso il teorema di Gauss.
q = ε E A = ε E 2π r L da cui E = q / (ε 2π r L)
Ricordiamo ora che E = -grad V e da cui
otteniamo
e quindi
continua.....


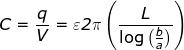


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor



