



Sempre devi avere in mente Itaca, raggiungerla sia il pensiero costante.
LA LEGGE DI OHM (2)


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!



LA POTENZA
L'unità di energia elettrica è il watt ( W ) , dal nome di
James Watt ( 1736-1819 ).
Un watt di potenza è uguale al lavoro fatto
in un secondo dalla differenza di
potenziale di un volt
muovendo una carica di un coulomb.
Ricordando che 1 Coulomb al secondo è 1 Ampere,
avremo che la potenza in Watt equivale al
prodotto di Ampere per Volt .
Potenza in Watt = Volt x Ampere
P = E x I

Esempio : Un tostapane prende 5 A dalla linea di alimentazione 240V .
Quanta potenza viene utilizzata ? P = E x I = 240 V x 5 A P = 1200 Watt
Esempio : quanta corrente scorre nel filamento di una lampadina da 75 watt
collegato alla casalinga alimentazione di 240 Volt ?
Abbiamo la P (potenza ) ed E (volt) . Abbiamo detto che P = EI, da cui si ottiene :
I = P / E e pertanto : I = 75/240 I = 0,3125 Ampere, il risultato cercato
Questa quantità di corrente risulta meglio espressa in milliampere . Per convertire
ampere a milliampere occorre moltiplicare per 1000 . Questo ci darà : 312,5 mA
La Potenza in Watt può anche essere calcolata da :
, si legge , "la potenza è uguale al quadrato di I per R" .
, si legge , "la potenza è al quadrato di E diviso per R"


Watts e Unità di Potenza .
746 W = 1 CV Cavallo (HP Horse Power).
Questa relazione può essere ricordata più facilmente come 1 Cavallo equivale a
circa 3/4 kilowatt . Ricordo che 1 kilowatt = 1000 W.
LAVORO
Lavoro = Potenza sviluppata in un determinato Tempo
A partire dal Watt, possiamo sviluppare diverse altre unità importanti . Il principio
fondamentale da ricordare è che la Potenza è il Lavoro sviluppato in un lasso di tempo t,
mentre il Lavoro è la Potenza sviluppata in un determinato Tempo .
Le formule sono :
Potenza = lavoro / tempo e Lavoro = potenza x tempo
Con il Watt per unità di potenza, un watt usato nel tempo di un secondo è uguale al
lavoro di un joule . Per dirla semplicemente , 1 watt è 1 joule al secondo.
Pertanto , 1 W = 1 J / s .
il joule (J) è l'unità base del lavoro o energia .
Un'unità di lavoro che può essere utilizzata con singoli elettroni è l' elettronvolt . Si
noti che l'elettrone è la carica , mentre la tensione è la differenza di potenziale .
Ora 1eV ( si legge un elettronvolt) è la quantità di lavoro necessaria per spostare un
elettrone tra due punti aventi una differenza di potenziale di un volt .
Poiché elettroni equivalgono ad 1C e un joule è un Volt -Coulomb , ci
devono essere eV in 1J .
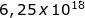
Chilowattora
Si tratta di un'unità comunemente usato per grandi quantità di lavoro elettrico o
energia .
La quantità viene calcolata semplicemente come il prodotto della potenza in
chilowatt moltiplicata per il tempo in ore durante le quali viene utilizzata la potenza .
Questa è l'unità di energia che devi sapere .
Esempio : Una lampadina utilizza 100 W o 0,1 kW per 4 ore ( h ), la quantità di
energia utilizzata è :
Kilowattora = chilowatt x ore = 0,1 x 4 = 0.4 kWh .
Noi paghiamo la nostra energia elettrica domestica in chilowattora di energia .
POTENZA dissipata in una RESISTENZA
Quando la corrente fluisce in una resistenza , del calore viene prodotto a causa
dell'attrito tra il movimento degli elettroni liberi e gli atomi che ostruiscono il percorso
del flusso di elettroni .
Il calore è la prova che la Potenza viene usata nella produzione di corrente.
Questo è il modo per rompere un fusibile , dovuto al calore della eccessiva corrente
che fonde il filo di metallo nel fusibile .
La potenza è generata dalla sorgente di tensione applicata e consumata nella resistenza
sotto forma di calore . Questa potenza che la resistenza dissipa in calore deve essere fornita
dal generatore di tensione , altrimenti non può mantenersi la differenza di potenziale
necessaria per produrre la corrente .
Una qualsiasi delle tre formule può essere utilizzata per calcolare la potenza dissipata in una
resistenza . Quella da utilizzare è solo una questione di convenienza, a seconda di quali
fattori sono noti .
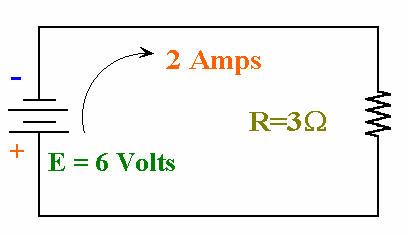
Nella figura, la potenza dissipata con 2 A attraverso la resistenza e con 6 V ai suoi
capi è 2 x 6 = 12 W. Oppure, calcolando in termini di corrente e resistenza ,
otteniamo
volte 3 , 4 x 3, che equivale a 12 W. Utilizzando invece la tensione e la
resistenza , la potenza può essere calcolata come
(o 36) , diviso 3 , che è
sempre uguale a 12 W.
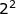
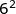
= 6 x 2 =12 W
= 2 x 2 x 3 =12 W
= 6 x 6 : 3 =12 W


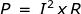
Nella figura di sopra, abbiamo introdotto un nuovo simbolo schematico : il simbolo
schematico di una batteria che vedete sulla sinistra . Si noti la piccola barra in alto è
il terminale negativo . La direzione del flusso di corrente è mostrata correttamente ,
da negativo a positivo
Non importa quale equazione avrete utilizzata , 12 W di potenza vengono comunque
dissipati sotto forma di calore . La batteria deve generare questa quantità di potenza
continua al fine di mantenere la differenza di potenziale di 6 V che produce la corrente 2 A
sulla resistenza di 3 Ohm
In alcune applicazioni pratiche, la dissipazione di potenza elettrica è desiderabile perché
rappresenta la componente che deve produrre calore per fare il suo lavoro .
Per esempio , un tostapane da 600 W deve dissipare questa quantità di energia per produrre
la quantità di calore necessaria alla tostatura del pane. Allo stesso modo, una lampadina da
300 W deve dissipare il potere di rendere il filamento incandescente modo che avrà il bagliore
che fornisce la luce . In altre applicazioni, tuttavia , il calore può essere solo un indesiderabile
sottoprodotto della necessità di fornire corrente attraverso la resistenza in un circuito. In ogni
caso , però, quando c'è corrente in una resistenza , si dissipa una potenza pari a .
Il termine viene utilizzato più volte per descrivere indesiderate perdite di potenza
in un circuito resistivo .




Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor



