



I giovani adulti sono insicuri e incapaci di assumersi responsabilità in piena autonomia
ELETTRONICA


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!

Massa
kilogrammo
kg
RISOLUZIONE DI RETI INDUTTIVE NEL PERIODO TRANSITORIO




Risoluzione di reti induttive nel periodo transitorio
Verranno esaminate reti elettriche con un solo induttore,
di induttanza costante. Non si considererà la presenza
contemporanea di più induttori e quindi l’unico fenomeno
elettromagnetico di cui tener conto è l’autoinduzione.
Per risolvere la rete nel periodo transitorio di magnetizza-
-zione e smagnetizzazione dell’induttore, durante il quale le
grandezze elettriche (corrente e tensione) nel lato contene-
-nte l’induttore variano nel tempo con legge esponenziale,
bisogna calcolare tre elementi caratteristici di tali grandezze:
il valore iniziale, il valore finale e la costante di tempo, noti i
quali si ricavano le leggi di variazione della corrente e della
tensione indotta mediante le formule generali .
Per il calcolo della resistenza del circuito di magnetizzazione
o di smagnetizzazione che compare nell’espressione della
costante di tempo si ricorre generalmente alla determinazione del generatore equivalente di
Thevenin del relativo circuito.
Occorre inoltre tener presente la durata del funzionamento: se l’induttore resta collegato al
circuito di magnetizzazione o di smagnetizzazione per un tempo non inferiore a 4,6τ, si
può considerare che la corrente e la tensione siano arrivate ai valori di regime, altrimenti
occorre calcolarne i valori nell’istante in cui si ha la variazione di configurazione del circuito.
Per quanto riguarda gli altri elementi della rete, occorre valutare se il loro comportamento
sia oppure no influenzato direttamente dall’induttore: per esempio la tensione in un
resistore collegato in serie con un induttore, data da v = Ri, segue l’andamento
esponenziale della corrente.
Gli esempi seguenti hanno lo scopo di chiarire quanto precedentemente esposto

Esempio: Per la rete della sottostante figura, calcolare, dopo la chiusura dell’interruttore T,
la costante di tempo del circuito di magnetizzazione e gli andamenti della corrente
e della tensione sull’induttanza, disegnandone i relativi grafici.
Determinare, inoltre, l’andamento della corrente nel resistore R2, sia prima che
dopo la chiusura di T.
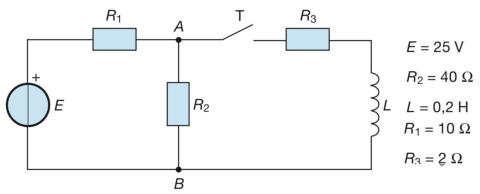
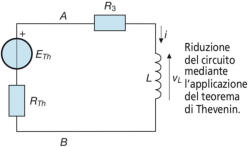
Con l’applicazione del teorema di Thevenin alla rete a sinistra dell’interruttore, si
ottiene:
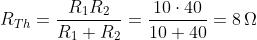
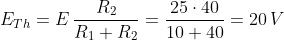
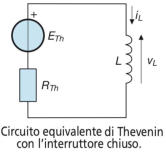
Il circuito equivalente è riportato nella figura a sinistra.
Il valore della costante di tempo è dato da:
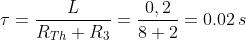
Poiché a regime l’induttanza si comporta come un cortocircuito, il valore finale della
corrente i è uguale a
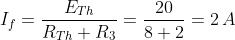
La corrente aumenterà esponenzialmente da zero a 2 A,
secondo la legge:
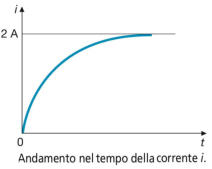
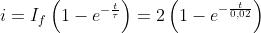
rappresentata nella figura alla tua destra.
La tensione indotta vL partirà dal valore iniziale VL0= ETh = 20 V (I0= 0) e tenderà
esponenzialmente a zero, secondo la legge:
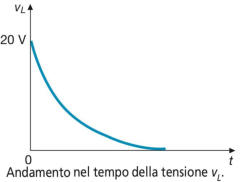
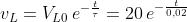
rappresentata destra
Per calcolare l’andamento della corrente in R2,
si considerino i sottostanti a) e b), rappresentanti,
rispettivamente, la rete data prima della chiusura di T e dopo tale
chiusura, in condizioni di regime, con l’induttanza sostituita da un cortocircuito.
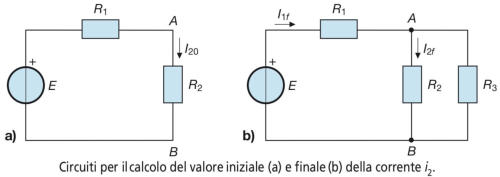
Si ricava:
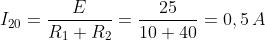
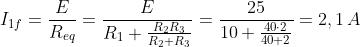
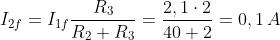
La corrente i2 diminuirà esponenzialmente da 0,5 A a 0,1 A, con la seguente legge:
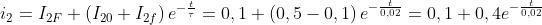
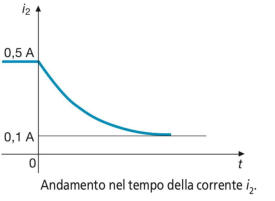
il cui grafico è riportato nella figura a destra

Esempio: Per il circuito della sottostante figura D3.16, a regime con l’interruttore aperto,
calcolare le correnti i1, i2, iL e la tensione vL e disegnarne gli andamenti nel tempo,
prima e dopo la chiusura dell’interruttore
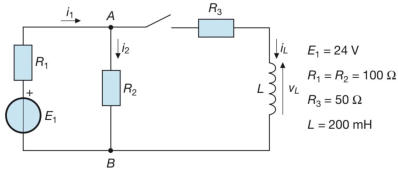
Interruttore aperto
La corrente nell’induttore è nulla, essendo il ramo aperto; anche la tensione vL
è nulla, dato che l’induttore si comporta a regime come un cortocircuito.
Nella maglia a sinistra dell’interruttore le due correnti sono uguali, essendo le resistenze
in serie. Si avrà quindi:
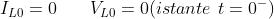
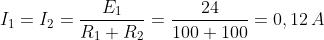
Interruttore chiuso
Applicando il teorema di Thevenin si ottiene il sottostante circuito equivalente, per il quale
si ha:
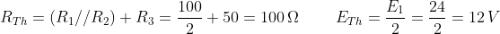
Il valore della costante di tempo è dato da:
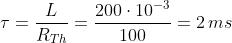
La corrente iL avrà un andamento esponenziale crescente, da zero al valore finale:
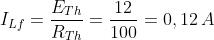
secondo la legge:
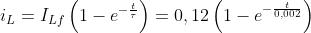
La tensione indotta partirà, all’istante
, dal valore iniziale e tenderà
esponenzialmente a zero, con legge:
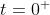
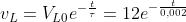
Con l’interruttore chiuso la tensione vAB sarà data da:
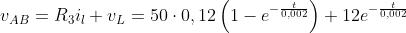
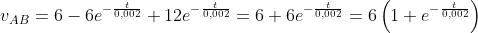
legge che indica un andamento esponenziale decrescente da 12 V (
) a 6 V (
).
Applicando la legge di Ohm e il primo principio di Kirchhoff, si calcolano gli andamenti
delle correnti i1 e i2:
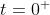
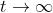
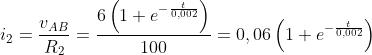
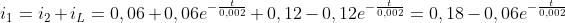
Per
gli esponenziali assumono il valore 1 e si ha:
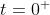

che sono esattamente i valori che avevano le due correnti prima della chiusura
dell’interruttore.
Per
gli esponenziali si annullano e si ricavano i valori di regime delle due
correnti:
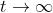
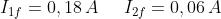
Si può notare che è rispettata la condizione I1f= I2f+ ILf stabilita dal primo principio di
Kirchhoff
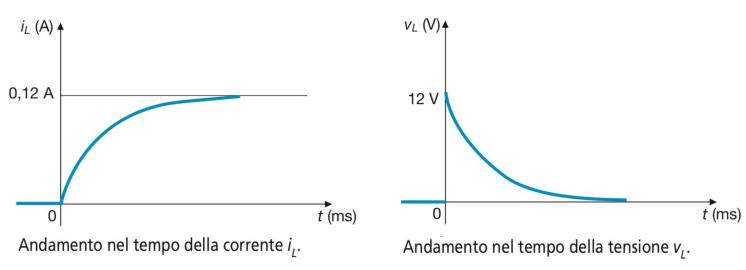
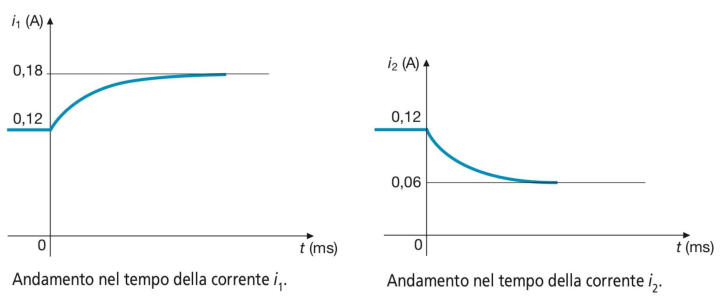
Gli andamenti richiesti delle correnti e della tensione sono riportati nelle sottostanti figure:


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





