Comportati sempre in modo da aumentare le possibilità di scelta.

ELETTRONICA

… studiare, studiare ed ancora studiare, è il solo modo di capire quanto possa essere grande sia la propria ignoranza!

Massa

kilogrammo

ESERCIZI DI VERIFICA

Esercizio 1 Nello schema della sottostante figura, il conduttore H-K ha una resistenza propria R2 e si muove di moto rettilineo uniforme entro un campo magnetico di induzione B costante. Calcolare: la velocità del conduttore; la tensione indotta; la forza esercitata dal campo sul conduttore, specificando se è motrice o resistente; la tensione Vhk, le potenze elettriche e il rendimento del sistema in movimento. Supponendo di invertire il senso del moto, calcolare i nuovi valori della corrente e della forza

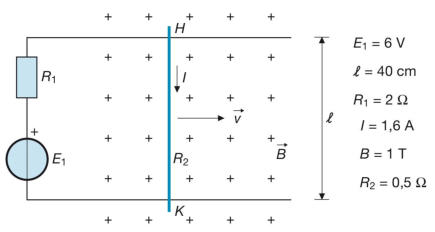
[Risultati: v = 5 m/s; E2= 2 V; F = 0,64 N (motrice); VHK = 2,8 V; Pa= 4,48 W; Pu= 3,2 W; Pp= 1,28 W; η = 0,714; I′= 3,2 A; F′= 1,28 N, resistente]

Esercizio 2 Nello schema della sottostante figura, il conduttore H-K ha una resistenza propria Ri e si muove di moto rettilineo uniforme entro un campo magnetico di induzione B costante. Calcolare: la forza esercitata dal campo sul conduttore, specificando se è motrice o resistente; la tensione indotta sul conduttore; la tensione VHK; le resistenze Ri e R; le potenze elettriche del sistema in movimento.

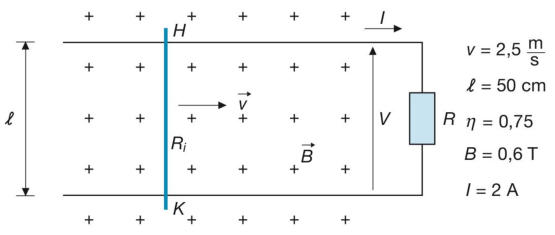
[Risultati: F = 0,6 N (resistente); E = 0,75 V; VHK = 0,563 V; Ri= 0,0937 Ω; R = 0,281 Ω; Pg= 1,5 W; Pu= 1,125 W; Pp= 0,375 W]

Esercizio 3 Per la bobina sotto raffigurata, interessata da un campo magnetico di induzione B costante, calcolare: la coppia prodotta dal campo, con la bobina nella posizione di figura; la forza agente su ogni conduttore; la forza agente su ogni lato; la coppia massima che il campo può produrre sulla bobina, specificando in quale posizione si ha tale coppia; la corrente necessaria per produrre la stessa coppia se l’angolo α vale 30° anziché 45°

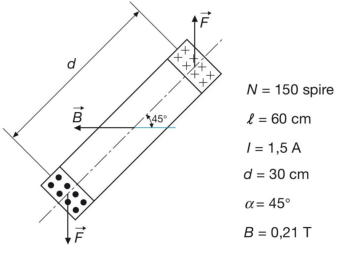
[Risultati: C = 6 Nm; Fc= 0,189 N; Fl= 28,4 N; CM= 8,5 Nm; I′= 1,22 A]

Esercizio 4 Calcolare la coppia agente sulla bobina dell’esercizio 3, nel caso di campo magnetico con linee di forza radiali. [Risultato: C = 8,5 N]

Esercizio 5 Determinare la forza elettrodinamica che si origina tra due conduttori a barra, lunghi 10 m, di sezione rettangolare 5 × 20 mm, posti in aria alla distanza di 20 cm, quando la densità di corrente in ognuno di essi è di 5 A/mm2. [Risultato: F = 2,5 N]

Esercizio 6 Calcolare la forza di cui all’esercizio precedente, nel caso che, in seguito a un cortocircuito, la corrente nelle barre diventi 20 volte maggiore di quella che si ha nel funzionamento normale. [Risultato: F = 1000 N]

Esercizio 7 Una spira elettrica, di dimensioni 10 × 15 cm, ruota con velocità angolare costante in un campo magnetico uniforme di induzione B = 1,3 T. Calcolare: il flusso magnetico massimo concatenato con la spira; la velocità di rotazione, espressa in giri/min, per avere nella spira una EM = 2 V. [Risultati: ΦM= 19,5 mWb; n = 980 giri/min]

Esercizio 8 Su un nucleo chiuso di materiale ferromagnetico con traferro, avente permeabilità relativa μr = 1200 supposta costante, lunghezza della parte in ferro 60 cm, lunghezza del traferro 0,3 mm, sezione trasversale 10 cm2, sono montate due bobine con N1 = 500 spire ed N2 = 800 spire, con coefficiente di accoppiamento k = 0,8. Calcolare:le induttanze delle bobine; il coefficiente di mutua induzione; le tensioni indotte nelle due bobine quando nella prima la corrente circolante, pari a 2 A, si annulla linearmente in 10 ms e la seconda bobina è aperta. [Risultati: L1= 0,393 H; L2= 1 H; M = 0,501 H; E1= − 78,5 V; E2= − 100 V]

Esercizio 9 Due bobine, aventi rispettivamente N1 = 400 spire e N2 = 250 spire, mutuamente accoppiate al 75%, sono montate su un nucleo magnetico di riluttanza totale 358,1 kH−1. Calcolare: le induttanze delle due bobine; il coefficiente di mutua induzione; le tensioni indotte quando nella prima bobina la corrente varia secondo il sottostante grafico e la seconda bobina è aperta

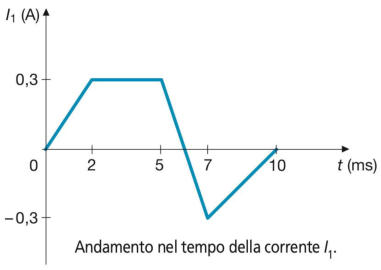
[Risultati: L1= 0,447 H; L2= 0,175 H; M = 0,21 H; E1: 67 V, 0 V, – 134 V, 44,7 V; E2: 31,5 V, 0 V, − 63 V, 21 V]

Esercizio 10 Su due bobine mutuamente accoppiate sono state svolte le seguenti prove: a) tenendo aperta la seconda bobina e facendo aumentare linearmente la corrente nella prima da zero a 10 A in 0,1 s, sono state misurate le tensioni indotte E1 = 10 V e E2 = 6 V; b) tenendo aperta la prima bobina e facendo aumentare linearmente la corrente nella seconda da zero a 10 A in 0,1 s, sono state misurate le tensioni indotte E1 = 6 V e E2 = 5 V. Calcolare: le induttanze delle due bobine; il coefficiente di mutua induzione; il fattore di accoppiamento;il numero di spire della seconda bobina, sapendo che N1 = 300 spire. [Risultati: L1= 0,1 H, L2= 0,05 H, M = 0,06 H; k = 0,849; N2= 212 spire]

Lorem Ipsum Dolor

Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.

Add your one line caption using the Image tab of the Web Properties dialog

Made with Xara