



Dei quadri moderni si capisce una sola cosa: la firma
ELETTRONICA


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!


Massa
kilogrammo
kg
MUTUA INDUZIONE


MUTUA INDUZIONE
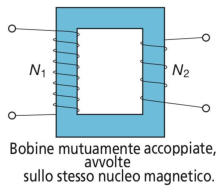
Nella figura sottostante, sono rappresentate due bobine
di N1 e N2 spire, avvolte sullo stesso nucleo magnetico.
Le due bobine sono mutuamente accoppiate, in quanto la
circolazione di corrente in una delle due produce un flusso
magnetico nel nucleo, che va a interessare, in tutto o in
parte, anche l’altra bobina. Questo è quanto avviene, per
esempio, nei trasformatori elettrici.

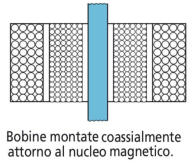
Nella pratica costruttiva, per migliorarne l’accoppiamento, le due
bobine vengono spesso disposte in modo coassiale, una all’interno
dell’altra (come indicato nella figura alla tua sunistra).
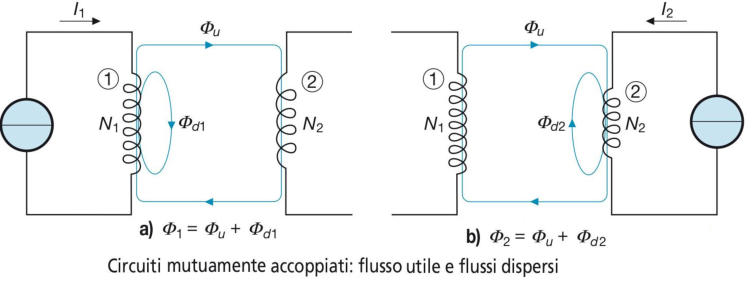
Nelle sottostanti figure a) e b) è riportato lo schema di due bobine
mutuamente accoppiate, nei casi in cui è alimentata la bobina 1 e
l’altra è aperta e viceversa.
I flussi magnetici che compaiono nello schema hanno il seguente significato:
• nel caso (a il flusso Φu è il flusso utile che, prodotto dalla bobina 1, va a interessare
anche tutte le spire della bobina 2; il flusso Φd1 è, invece, il flusso disperso che,
prodotto dalla bobina 1, non si richiude entro nessuna spira della bobina 2; Φ1 è il
flusso totale della bobina 1, somma dei due flussi;
• nel caso (b il flusso Φu è ancora il flusso utile, questa volta prodotto dalla bobina 2
e che si richiude in tutte le spire della bobina 1; il flusso Φd2 è, invece, il flusso disperso
che, prodotto dalla bobina 2, non si richiude entro nessuna spira della bobina 1; Φ2 è il
flusso totale della bobina 2, somma dei due flussi.

Considerando il caso della soprastante figura (a) e applicando la legge di Hopkinson e la
relazione , si ricava l’espressione del flusso totale prodotto dalla bobina 1:
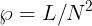
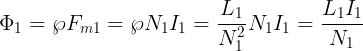
Il flusso utile che si richiude nella bobina 2 è una parte di questo flusso; introducendo il
coefficiente adimensionato , variabile tra 0 (flusso utile nullo) e 1
(flusso utile uguale a quello totale e quindi flusso disperso nullo), si ottiene:
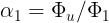
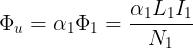
Il flusso concatenato con la bobina 2 è dato da:
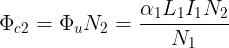
Si definisce coefficiente di mutua induzione M il rapporto tra il flusso concatenato
con la bobina 2 e la corrente della bobina 1 che l’ha prodotto:
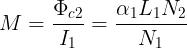
Ripetendo il ragionamento precedente per il caso della figura (b) è facile verificare che il
coefficiente di mutua induzione tra le bobine, pari in questo caso al rapporto
sarà dato da:

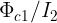
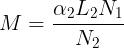
Moltiplicando membro a membro le ultimr due espressioni si ha:

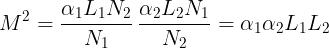
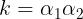
Indicando con il coefficiente o fattore di accoppiamento tra le due bobine, si
ottiene infine:

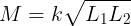
relazione che lega il coefficiente di mutua induzione alle induttanze delle due bobine e
al loro fattore di accoppiamento.
Il coefficiente k è un numero adimensionato, per cui l’unità di misura di M è la
stessa dell’induttanza, cioè l’henry (H).
Se le due bobine hanno la stessa induttanza L si ricava facilmente la relazione M = kL.
Riguardo i valori che può assumere il fattore di accoppiamento, si ha che:
• k = 0 (M = 0) indica che l’accoppiamento tra le bobine è nullo e quindi nessuna linea di
flusso prodotta dall’avvolgimento magnetizzante si concatena con l’altro;
• k = 1 ( ) indica che l’accoppiamento tra le due bobine è perfetto, in
quanto tutto il flusso prodotto da una bobina si concatena con l’altra (flussi dispersi nulli).
L’accoppiamento è tanto più stretto quanto più k si avvicina a 1, tanto più debole o
lasco quanto più il valore di k è prossimo a zero
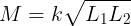

Esempio : Calcolare il coefficiente di mutua induzione tra due bobine le cui induttanze
sono L1 = 0,1 H e L2 = 25 mH, con coefficiente di accoppiamento 75%.
Utilizzando la nota relazione con k = 0,75, si ricava:
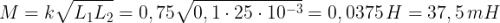

Tensione indotta per mutua induzione
Se nel circuito della soprastante figura (a) la corrente I1 viene resa variabile nel tempo,
accadono due fenomeni di induzione elettromagnetica:
• nella bobina 1 nasce una tensione per autoinduzione, dovuta alla variazione di I1 , in
modo analogo a quanto visto nel paragrafo precedente;
• nella bobina 2 nasce una tensione di mutua induzione, dovuta alla variazione del
flusso concatenato Φc2, variazione conseguente a quella di I1 ; l’avvolgimento 1 è
detto induttore in quanto produce la variazione di flusso, mentre l’avvolgimento 2
è detto indotto, dato che subisce gli effetti di tale variazione.
Indicando con ΔI1 la variazione della corrente nell’intervallo di tempo Δt e supponendo
M costante, la variazione del flusso concatenato con la bobina 2, è pari a:
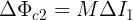

e, quindi, la tensione indotta nella bobina 2 sarà data, per la legge di Faraday-
Neumann, da:
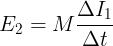
Come si vede, è stata usata l’espressione senza il segno “−”; però si deve sempre
tener conto della legge di Lenz e quindi la polarità di E2 deve essere tale da opporsi
alla variazione del flusso concatenato Φc2.
Per capire come va applicata la legge di Lenz in questo caso, si consideri lo schema
disegnato qui sotto, in cui si suppone che entrambe le bobine siano avvolte in senso
antiorario e che la bobina 2 sia chiusa su un resistore.
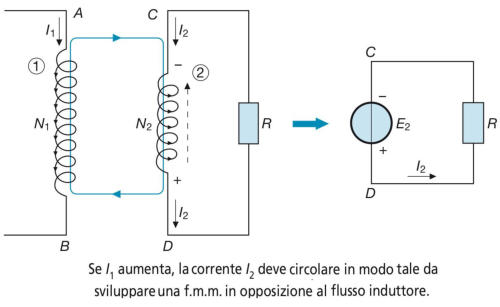
Se I1 aumenta (ΔI1> 0) per l’equazione conosciuta, si ha E2> 0; tale tensione deve far
circolare nel secondario la corrente I2 in modo che essa, attraversando la bobina 2,
produca un flusso di reazione diretto verso l’alto, opposto al flusso induttore che sta
aumentando; ciò avviene se la tensione E2 è positiva in D e negativa in C.
Si può anche dire, più correttamente, che la f.m.m. di reazione N2I2 deve essere
smagnetizzante, in modo da opporsi all’aumento della f.m.m. N1I1.
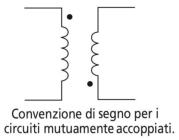
Per evitare possibili confusioni dovute al senso di avvolgimento delle
bobine che, cambiando, fa variare il senso del flusso, viene adottata
la seguente convenzione per i circuiti mutuamente accoppiati come
nella figura a destra: quando la corrente entrante nel morsetto
segnato con il pallino di una bobina aumenta, la tensione mutua-
-mente indotta nell’altra è positiva sul corrispondente morsetto
segnato. Ovviamente se la corrente entrante nel morsetto segnato
diminuisce, si inverte la polarità della tensione indotta
Il fenomeno della mutua induzione è molto importante ed è alla base del unzionamento di
molte macchine elettriche: sfruttando questo fenomeno è possibile trasferire energia
elettrica tra due circuiti elettricamente separati, dato che la variazione della corrente in
un circuito fa nascere tensione nell’altro (e anche corrente, se il circuito è chiuso).

Esempio: Tra due bobine le cui induttanze sono L1 = 0,1 H e L2 = 25 mH, con coefficiente
di accoppiamento 75% si calcolino le tensioni indotte di auto e mutua
induzione che si hanno quando la corrente nella prima bobina subisce una
variazione incrementale di 50 A/s.
Il dato 50 A/s corrisponde al rapporto incrementale ΔI1/Δt. Nella prima bobina si
ha una tensione di autoinduzione, mentre nella seconda avviene un fenomeno di
mutua induzione. Le due tensioni indotte saranno pari a:

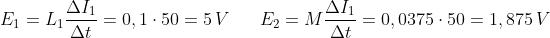


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





