



In amore ci vuole fortuna e comunque anche un bel culo non guasta
ELETTRONICA


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!

Massa
kilogrammo
kg
AUTOINDUZIONE E MUTUA UNDUZIONE


Autoinduzione
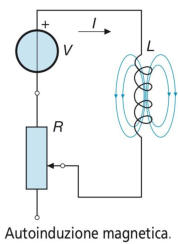
Si consideri la sottostante figura, un induttore di induttanza
L costante, inserito in un circuito in cui è possibile variare la
corrente circolante I.
Il flusso concatenato con l’induttore è dato da Φc= LI ed è
variabile nel tempo con la corrente.
L’induttore sarà soggetto a un flusso concatenato variabile,
prodotto dalla sua stessa corrente, e quindi ai suoi capi
nascerà una tensione per autoinduzione magnetica, dove il
termine “autoinduzione” indica che la causa del fenomeno
induttivo è da imputare allo stesso circuito che ha prodotto
il flusso magnetico.
Indicando con ΔΦc la variazione del flusso concatenato
nell’intervallo di tempo Δt, dovuta alla variazione ΔI della
corrente, si avrà:
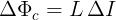
e, quindi, la tensione indotta per autoinduzione nella bobina sarà
data da , da cui si ricava immediatamente:
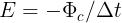
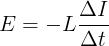
formula in cui compare il rapporto incrementale ΔI/Δt, che può
essere interpretato come la velocità di variazione della corrente nel
tempo, analogamente al rapporto Δs/Δt che rappresenta la velocità
di un corpo che percorre lo spazio Δs nel tempo Δt.
Dall’esame della relazione, si deduce che il valore della tensione di
autoinduzione è direttamente proporzionale all’induttanza della
bobina e alla velocità di variazione della corrente; quanto più la corrente nel circuito varia
rapidamente, tanto maggiore è l’incremento (o il decremento) ΔI nello stesso intervallo di
tempo Δt e tanto maggiore sarà la tensione indotta.
Considerando un intervallo infinitesimo di tempo dt, a cui corrisponde la variazione
di, il rapporto incrementale diventa la derivata di/dt della corrente rispetto al tempo e
la relazione assume la forma:
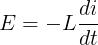
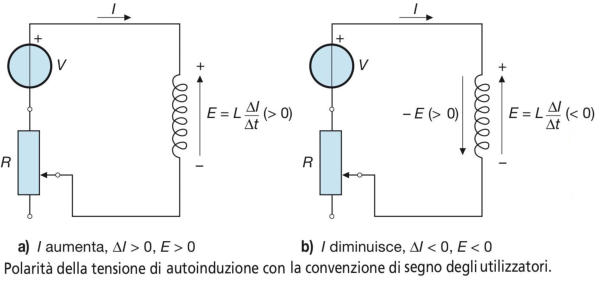
In merito alla polarità della tensione indotta va precisato che:
•
se la corrente aumenta, si ha ΔI > 0 e quindi dalla relazione, essendo L e Δt entrambi
positivi, si ricava E < 0; la tensione indotta, per la legge di Lenz, deve opporsi
all’aumento della corrente e quindi dovrà avere la polarità indicata nella figura (a, in
modo che il verso effettivo della tensione (– E), positiva, sia in opposizione alla corrente;
se la corrente diminuisce, si ha ΔI < 0 ed E > 0; la tensione indotta deve opporsi
•
alla diminuzione della corrente, favorendone la circolazione nella maglia e quindi dovrà
avere la polarità indicata nella figura (b.
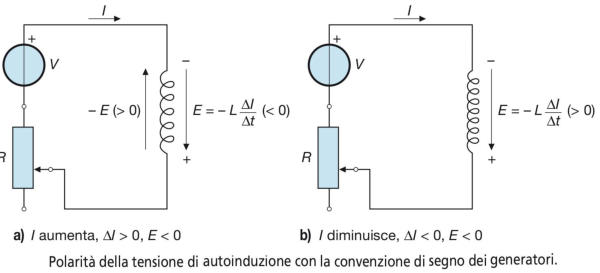
In entrambi i casi la corrente esce dal “+” della tensione indotta, secondo la
convenzione di segno dei generatori. Dato che nelle reti elettriche gli induttori sono
considerati come utilizzatori, conviene usare la convenzione di segno di questi
ultimi, con corrente entrante dove c’è il “+” della tensione indotta; per far questo occorre
considerare le suaccennate espressioni senza il segno “–”, ottenendo:
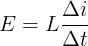
Le polarità della tensione indotta sono indicate nelle sottostanti figure a) e b).

Esempio: La corrente in una bobina di induttanza L = 10 mH aumenta linearmente da
0 a 5 A in 5 ms, rimane poi costante per 10 ms e si annulla nei successivi 20 ms.
Calcolare la tensione indotta e l’impulso di tensione nei tre intervalli di tempo
indicati.
Le variazioni di corrente nei tre intervalli sono date da:
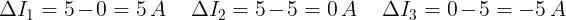
Applicando le relazioni conosciute, si ha:
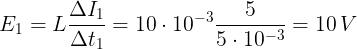
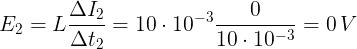
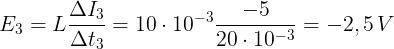
Per ogni intervallo di tempo l’impulso di tensione è dato da: U = EΔt = LΔI e, quindi, si ha:
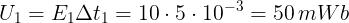
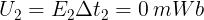
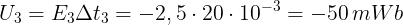
Sommando i tre valori si ottiene zero, dato che la variazione totale di corrente è nulla.
Nella figura D2.30 sono riportati gli andamenti nel tempo della corre
Nella figura D2.30 sono riportati gli andamenti nel tempo della corrente e della tensione
indotta; le aree del grafico E = f(t) rappresentano gli impulsi di tensione.
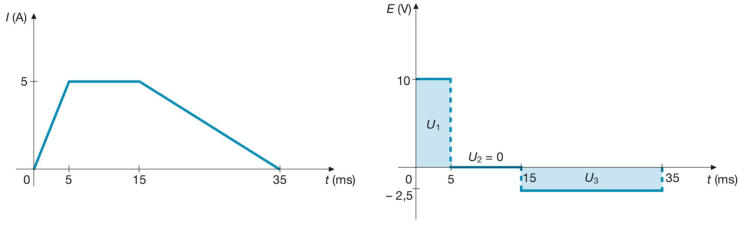
Si può notare che la tensione indotta è maggiore nei tratti in cui la pendenza del grafico di
I(t) è più accentuata, mentre è nulla nei tratti in cui la corrente è costante. Inoltre, la
tensione è positiva quando la corrente aumenta e viceversa


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





