



Talvolta parlare al vento giova più che comunicare con certa gente.
ELETTRONICA


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!

Massa
kilogrammo
kg
TENSIONE INDOTTA IN UNA SPIRA ROTANTE


Tensione indotta in una spira rotante
in un campo magnetico
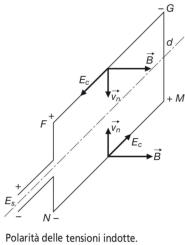
Si supponga che una spira aperta di forma rettangolare,
come in figura, di dimensioni l e d, venga posta in rotazione
con velocità angolare ω costante all’interno di un campo
magnetico di induzione costante, con linee di forza
perpendicolari all’asse della spira.
Il movimento della spira presuppone
che sulla stessa agisca una coppia
motrice, in grado di produrne la
rotazione. Si ipotizza, inoltre, che
i lati FG e MN siano attivi durante
il movimento, mentre i lati FN e GM
siano posti fuori dal campo magne-
-tico.
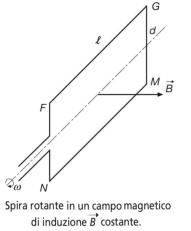
stessa, si ottiene la figura di sinistra, nella quale
la velocità
è quella periferica di ogni conduttore, legata
alla velocità angolare dalla relazione:
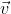
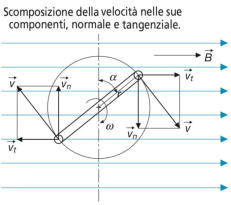
Rappresentando lo schema su un piano perpendicolare
alla spira
La componente della velocità che “taglia” le linee di flusso
è quella normale, perpendicolare alle linee di campo :
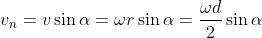
Su ogni conduttore attivo, in movimento all’interno del campo magnetico, nasce una
tensione indotta Ec, data dall’espressione:

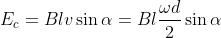
le cui polarità, individuate con la regola delle tre dita della mano destra, sono riportate
nella seguente figura a destra.
Le tensioni indotte nei due conduttori hanno lo stesso valore e
agiscono in modo concorde tra loro e quindi la tensione indotta
nella spira sarà la somma delle due:
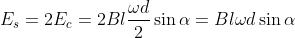
Essendo ld = S la sezione della spira, il prodotto Bld = BS = ΦM
rappresenta il flusso magnetico massimo che si può concatenare
con la spira, ossia il flusso che la spira abbraccia quando è
perpendicolare alle linee di campo (α = 0°).
Considerando inoltre che α è lo spostamento angolare della
spira rispetto alla posizione verticale di partenza (t = 0),
dato da α = ωt, e sostituendo nella Es, si ottiene:
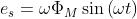
dove con la lettera minuscola è stato evidenziata la variabilità nel tempo della tensione
indotta.
Quest’ultima relazione è molto importante: da essa si vede che:
la tensione indotta in una spira che si muove di moto circolare uniforme in un
campo magnetico di induzione costante non è costante nel tempo, ma varia con la
funzione sen (ωt), ossia varia con legge sinusoidale.
Si è ottenuta, in questo modo, una tensione alternata sinusoidale.
Dato che il seno di un angolo può assumere al massimo il valore uno, indicando con
EM= ω ΦM il valore massimo della tensione sinusoidale, l’ultima equazione diventa:
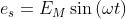
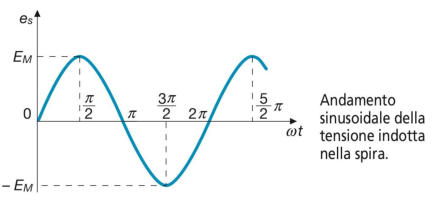
L’andamento nel tempo della tensione es è rappresentato nella sottostante figura :
la tensione varia periodicamente, riprendendo gli spessi valori a ogni giro della spira.
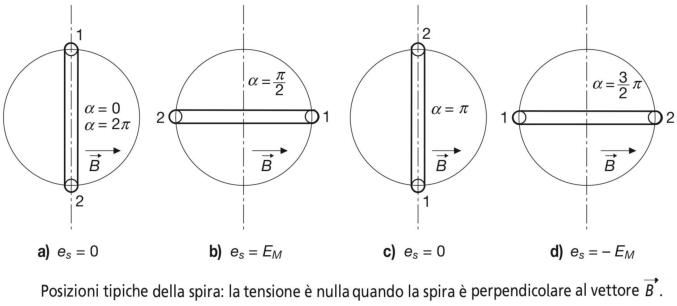
Le posizioni della spira relative ai valori ,
sono riportate nelle sottostanti figure a), b), c) e d).
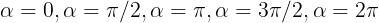
In merito ai fenomeni elettromagnetici che si hanno nel caso della spira rotante, si
possono ripetere le considerazioni fatte per il conduttore in movimento traslatorio;
brevemente si può osservare che:
•
si ha tensione indotta anche se la spira è ferma e ruota il campo magnetico, dato
che, anche in questo caso, conta la velocità relativa della spira rispetto al campo;
•
nel funzionamento da generatore la spira è posta in rotazione da un motore primo
esterno, che fornisce la coppia motrice e la potenza meccanica, mentre la spira
erogherà corrente (e, quindi, potenza elettrica) all’utilizzatore elettrico collegato ai
suoi capi (la tensione indotta si comporta da f.e.m.); su ogni lato della spira nascerà,
a causa del campo magnetico, una forza meccanica e quindi una coppia di forze
avente la funzione di coppia resistente;
•
nel funzionamento da motore la spira è alimentata da un generatore elettrico
esterno che fornisce la potenza elettrica (la tensione indotta si comporta da
f.c.e.m.); la coppia di forze generate dal campo magnetico ha funzione di coppia
motrice e pone in rotazione la spira che trasmette il suo moto al carico meccanico,
moto al quale si opporrà la coppia resistente del carico


Esempio: Calcolare la tensione massima che si ha in una spira che ruota con velocità di
1000 giri /min in un campo magnetico di induzione B = 1,2 T e ha una sezione di
200 cm2. Calcolare, inoltre, la tensione indotta dopo 1/8 di giro.
Una velocità di 1000 giri/min corrisponde a 1000/60 giri/s; dato che 1 giro = 2π
radianti, la velocità angolare sarà data da:
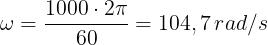
Il flusso massimo è pari a:
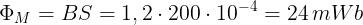
e, quindi, il valore massimo della tensione indotta è uguale a:
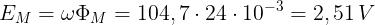
Dopo un ottavo di giro si ha e, quindi, la tensione indotta nella spira
sarà pari a
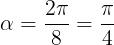
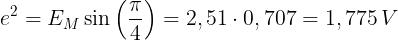


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





