



Non si muore. Si cessa soltanto di vivere
ELETTRONICA


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!


Massa
kilogrammo
kg
TENSIONE INDOTTA IN UN CONDUTTORE


Tensione indotta in un conduttore
in moto relativo rispetto al campo magnetico
Si consideri la sottostante figura, un conduttore elettrico che
si muove di moto rettilineo uniforme, con velocità costante v,
in un campo magnetico di induzione B costante, le cui linee
di forza sono tra loro parallele ed “entranti” perpendicola-
-rmente nel piano del disegno. Il conduttore è collegato,
mediante due guide conduttrici, a un resistore esterno
di resistenza R; si suppone che la resistenza propria del
conduttore e quella delle guide sia trascurabile rispetto a R.
Tutto il complesso costituirà una bobina con N = 1 spira, di
sezione S variabile in funzione della posizione del conduttore,
concatenata con un flusso Φc= NΦ = Φ = BS che sarà
anch’esso variabile con la sezione e quindi sul conduttore
verrà indotta una tensione che, comportandosi da f.e.m.,
farà circolare una corrente I, dato che il circuito è chiuso e
non vi sono altri generatori.
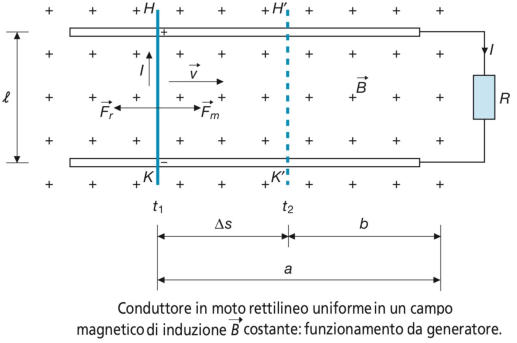
Se nell’intervallo di tempo Δt = t2– t1 il conduttore ha percorso lo spazio Δs = vΔt, la
variazione del flusso concatenato è stata pari a:
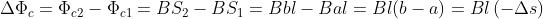
La tensione indotta è data da:
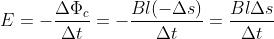
Il rapporto è pari alla velocità di traslazione del conduttore e quindi si avrà:
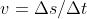
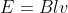
ossia:
la tensione indotta in un conduttore che si muove di moto traslatorio in un campo
magnetico di induzione costante è direttamente proporzionale ai valori dell’induzione
magnetica, della velocità e della lunghezza del conduttore interessato dalle
linee di flusso.
È facile constatare che allo stesso risultato si sarebbe arrivati facendo traslare le
linee di campo con il conduttore fermo, alla stessa velocità, ma in senso opposto;
questo perché la velocità che compare nella soprastante relazione è la velocità relativa
del conduttore rispetto al campo magnetico, pari alla differenza vettoriale tra le due
velocità.
Se entrambi i sistemi (circuito elettrico e magnete induttore) si muovessero alla stessa
velocità e nello stesso senso, non ci sarebbe tensione indotta, dato che il conduttore
risulterebbe fermo rispetto al campo magnetico.
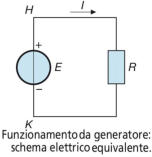
La presenza di una tensione in un circuito chiuso determina la circolazione di una corrente
che, per la legge di Lenz, deve opporsi alla causa che l’ha determinata.
Dato che, nel caso in esame, il flusso concatenato diminuisce, la corrente deve produrre
un campo magnetico avente lo stesso verso di quello preesistente e quindi deve circolare
in senso orario nella spira e dal punto K al punto H nel conduttore, come mostrato nella
soprastante figura.
Affinché la corrente possa circolare in questo senso, la tensione indotta deve comportarsi
da f.e.m., con la polarità positiva in H e negativa in K.
Il valore della corrente circolante è dato da:
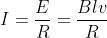
Si è ottenuto, in questo modo, un generatore elettrico elementare, che
forza la circolazione della corrente sul circuito esterno, dalla sua
polarità positiva a quella negativa, com nella figura a sinistra.
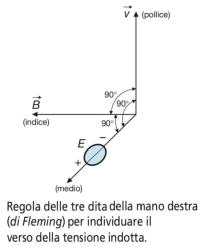
La polarità della tensione indotta può essere stabilita, oltre che con il ragionamento
precedente, anche con la regola di Fleming o delle tre dita della mano destra (figura
alla tua destra): disponendo il medio, l’indice e il pollice a 90° tra loro, vi è la seguente
corrispondenza:
•
medio
indica la polarità della grandezza elettrica
(tensione indotta)
•
indice
indica il verso della grandezza magnetica
(vettore induzione)
•
pollice
indica il verso della grandezza meccanica
•
(vettore velocità)
La circolazione della corrente nel conduttore fa nascere una
forza meccanica (conduttore percorso da corrente, posto in
un campo magnetico), diretta nella direzione del moto, ma
in verso opposto, in base alla già conosciuta regola della
mano sinistra richiamata nelle precedento pagine.
Tale forza è da intendere come forza resistente, in quanto opposta alla direzione del moto:
per far muovere il conduttore a velocità v costante occorre allora applicare una forza
motrice uguale e opposta a quella resistente esercitata dal campo, in modo da avere:




dato che v = costante implica un’accelerazione nulla.
Quanto descritto corrisponde al comportamento da generatore elettrico, al quale il sistema
meccanico esterno fornisce la forza motrice che determina il movimento della parte mobile,
movimento a cui si oppone il sistema elettromagnetico, mediante la forza resistente.
La tensione indotta si comporta da forza elettromotrice e determina la circolazione della
corrente elettrica verso l’utilizzatore esterno, così come avviene nei bipoli generatori.
Si consideri ora, nella sottostante figura, lo stesso precedente sistema, ma alimentato da
un generatore di corrente costante I.
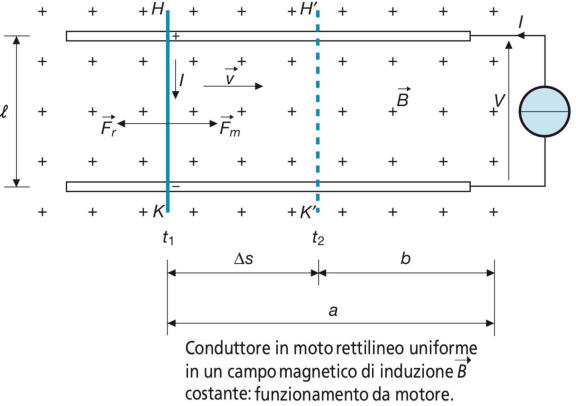
I fenomeni elettromagnetici che avvengono sono gli stessi, ma la loro sequenza logica
cambia. In particolare si ha che:

•
la corrente I, circolando da H verso K nel conduttore posto in un campo
magnetico, fa nascere una forza motrice Fm = BIl, diretta verso destra;
•
supponendo che questa forza motrice sia contrastata da una forza
resistente Fr applicata da un sistema meccanico esterno, uguale e
opposta a Fm, il conduttore si muoverà di moto rettilineo uniforme
verso destra;
•
sul conduttore, a causa della diminuzione del flusso concatenato con
la spira, nasce una tensione indotta E = Blv, positiva in H e negativa
in K, che si comporta come forza controelettromotrice, in quanto
contrasta la circolazione della corrente I del generatore; essa, infatti,
tenderebbe a creare una circolazione di corrente in senso orario nella
spira, in modo da rinforzare il flusso concatenato che è diminuito,
evidenziato nella seguente figura.
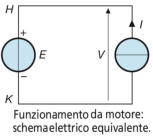
Si ottiene, in questo modo, il comportamento da motore elettrico in
cui il sistema elettromagnetico crea la forza motrice che determina
il movimento della parte mobile, movimento a cui si oppone il carico
meccanico collegato al motore, mediante la forza resistente.
La corrente elettrica deve essere fornita da un generatore esterno e
a essa si oppone la tensione indotta, così come avviene negli
utilizzatori attivi.
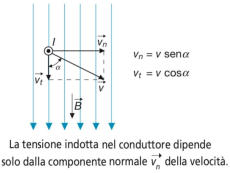
Se il conduttore (come in figura a destra) si muove nel campo
magnetico in direzione non perpendicolare alle linee di forza,
occorre scomporre il vettore velocità nelle seguenti componenti:
• velocità tangenziale vt = v cosα, che non produce alcuna
tensione indotta, in quanto origina un movimento che “non
taglia” le linee di flusso del campo e quindi non fa variare
il flusso concatenato;
• velocità normale vn = v senα, dalla quale dipende la
tensione indotta, essendo l’unica componente che determina la variazione del flusso
concatenato.
La precedente espressione diventa pertanto:
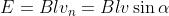

Esempio: Per il sistema elettromagnetico I=Blv/R, già visto, la corrente indotta è pari
a 5 mA, R = 1 kΩ, B = 1 T, l = 0,5 m. Calcolare la velocità normale di traslazione del
conduttore e la tensione indotta.
La tensione indotta è data da:
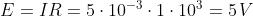
da cui, si ricava:
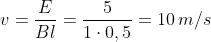


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





